
【题目】已如椭圆C:![]() 的两个焦点与其中一个顶点构成一个斜边长为4的等腰直角三角形.
的两个焦点与其中一个顶点构成一个斜边长为4的等腰直角三角形.
(1)求椭圆C的标准方程;
(2)设动直线l交椭圆C于P,Q两点,直线OP,OQ的斜率分别为k,k'.若![]() ,求证△OPQ的面积为定值,并求此定值.
,求证△OPQ的面积为定值,并求此定值.
【答案】(1)![]() ;(2)△OPQ的面积为定值,且此定值为
;(2)△OPQ的面积为定值,且此定值为![]() ,见解析
,见解析
【解析】
(1)根据等腰直角三角形可知,![]() ,根据
,根据![]() 求解椭圆方程;(2)当
求解椭圆方程;(2)当![]() 与
与![]() 轴垂直时,设
轴垂直时,设![]() ,代入
,代入![]() 和椭圆方程,得到面积,当
和椭圆方程,得到面积,当![]() 与
与![]() 轴不垂直时,设直线l的方程为
轴不垂直时,设直线l的方程为![]() ,联立方程,得到根与系数的关系,并表示面积,得到面积是定值.
,联立方程,得到根与系数的关系,并表示面积,得到面积是定值.
(1)设椭圆C的左、右焦点分别为F1,F2.依题查,有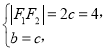 得
得![]() ,则
,则![]() ,
,
所以椭圆C的标准方程为![]() .
.
(2)证明:①当直线1与x轴垂直时,设直线l的方程为![]() ,
,![]() ,
,![]() .
.
由![]() ,且
,且![]() ,解得
,解得![]() ,
,![]() 或
或![]() ,
,![]() ,所以
,所以![]() .
.
②当直线l与x轴不垂直时,设直线l的方程为![]() ,
,![]() ,
,![]() .
.
联立直线l和椭圆C的方程,得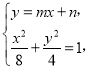 整理得
整理得![]() .
.
![]() ,
,![]() ,
,![]() .
.
由![]() ,则
,则![]() ,即
,即![]() ,
,
所以![]() ,
,
即![]() ,整理得
,整理得![]() ,则
,则![]() .
.
又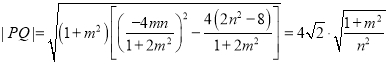 ,
,
点O到直线PQ的距离为![]() ,所以
,所以![]() .
.
综上,△OPQ的面积为定值,且此定值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为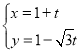 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,设
两点,设![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
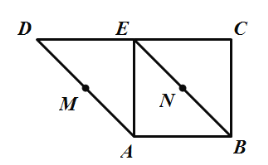
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,将三角形
的中点,将三角形![]() 沿
沿![]() 折起,则下列说法正确的是______________.
折起,则下列说法正确的是______________.
(1)不论![]() 折至何位置(不在平面
折至何位置(不在平面![]() 内),都有
内),都有![]() 平面
平面![]() ;
;
(2)不论![]() 折至何位置,都有
折至何位置,都有![]() ;
;
(3)不论![]() 折至何位置(不在平面
折至何位置(不在平面![]() 内),都有
内),都有![]() ;
;
(4)在折起过程中,一定存在某个位置,使![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一项自“一带一路”沿线20国青年参与的评选中“高铁”、“支付宝”、“共享单车”和“网购”被称作中国“新四大发明”,曾以古代“四大发明”推动世界进步的中国,正再次以科技创新向世界展示自己的发展理念.某班假期分为四个社会实践活动小组,分别对“新四大发明”对人们生活的影响进行调查.于开学进行交流报告会.四个小组随机排序,则“支付宝”小组和“网购”小组不相邻的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若数列![]() 满足,存在实数
满足,存在实数![]() ,对任意
,对任意![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 有上界,
有上界,![]() 是数列
是数列![]() 的一个上界,已知定理:单调递增有上界的数列收敛(即极限存在).
的一个上界,已知定理:单调递增有上界的数列收敛(即极限存在).
(1)数列![]() 是否存在上界?若存在,试求其所有上界中的最小值;若不存在,请说明理由;
是否存在上界?若存在,试求其所有上界中的最小值;若不存在,请说明理由;
(2)若非负数列![]() 满足
满足![]() ,
,![]() (
(![]() ),求证:1是非负数列
),求证:1是非负数列![]() 的一个上界,且数列
的一个上界,且数列![]() 的极限存在,并求其极限;
的极限存在,并求其极限;
(3)若正项递增数列![]() 无上界,证明:存在
无上界,证明:存在![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入3×3的方格中,使得每一行,每一列及对角线上的三个数的和都相等(如图所示),我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么不同的三阶幻方的个数是( )
4 | 9 | 2 |
3 | 5 | 7 |
8 | 1 | 6 |
A.9B.8C.6D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com