
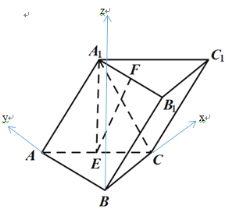
【题目】在斜三棱柱![]() 中,
中,![]() ,侧面
,侧面![]() 是边长为4的菱形,
是边长为4的菱形,![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
【答案】(1)证明见解析; (2) ![]() .
.
【解析】
(1)结合菱形的性质和勾股定理,证得![]() ,再由
,再由![]() ,得到
,得到![]() ,利用线面垂直的判定定理,即可证得
,利用线面垂直的判定定理,即可证得![]() 平面
平面![]() ;
;
(2)以![]() 为坐标原点,以射线
为坐标原点,以射线![]() 为
为![]() 轴,以射线
轴,以射线![]() 为
为![]() 轴,过
轴,过![]() 向上作平面的垂线为
向上作平面的垂线为![]() 轴建立空间直角坐标系,求得平面
轴建立空间直角坐标系,求得平面![]() 和
和![]() 的法向量,利用向量的夹角公式,即可求解.
的法向量,利用向量的夹角公式,即可求解.
(1)由题意,因为![]() 是菱形,
是菱形,![]() ,
,![]() 为
为![]() 中点,所以
中点,所以![]() .
.
又因为![]() 是直角三角形
是直角三角形![]() 的斜边
的斜边![]() 的中线,
的中线,
故![]() ,又
,又![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() 是直角三角形,∴
是直角三角形,∴![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)由(1)知![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
又由![]() ,所以
,所以![]() 平面
平面![]() ,
,
以![]() 为坐标原点,以射线
为坐标原点,以射线![]() 为
为![]() 轴,以射线
轴,以射线![]() 为
为![]() 轴,过
轴,过![]() 向上作平面
向上作平面![]() 的垂线为
的垂线为![]() 轴建立空间直角坐标系,如图所示,则
轴建立空间直角坐标系,如图所示,则![]() 轴,
轴,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
由(1)知![]() 平面
平面![]() ,∴平面
,∴平面![]() 的法向量
的法向量![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,![]() ,
,![]() ,
,
则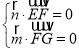 ,即
,即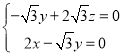 ,
,
令![]() ,则
,则![]() ,
,![]() .即
.即![]() ,
,
所以![]() ,
,
所以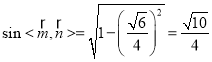 ,
,
故二面角![]() 的正弦值为
的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD-A1B1C1D1的底面为菱形,AA1⊥底面ABCD,∠BAD=120°,AB=2,E,F分别为CD,AA1的中点.
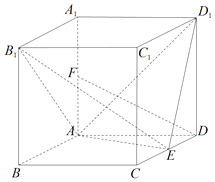
(Ⅰ)求证:DF∥平面B1AE;
(Ⅱ)若直线AD1与平面B1AE所成角的正弦值为![]() ,求AA1的长;
,求AA1的长;
(Ⅲ)在(Ⅱ)的条件下,求二面角B1-AE-D1的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有5个命题:
①函数![]() 的最小正周期是
的最小正周期是![]() ;
;
②终边在![]() 轴上的角的集合是
轴上的角的集合是![]() ;
;
③在同一坐标系中,函数![]() 的图象和函数
的图象和函数![]() 的图象有3个公共点;
的图象有3个公共点;
④把函数![]() 的图象向右平移
的图象向右平移![]() 得到
得到![]() 的图象;
的图象;
⑤角![]() 为第一象限角的充要条件是
为第一象限角的充要条件是![]() .
.
其中,真命题的编号是______(写出所有真命题的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
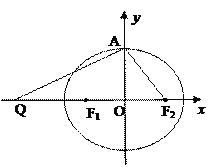
【题目】如图,设椭圆![]() 的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且
的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且![]() 0,若过 A,Q,F2三点的圆恰好与直线
0,若过 A,Q,F2三点的圆恰好与直线![]() 相切,过定点 M(0,2)的直线
相切,过定点 M(0,2)的直线![]() 与椭圆C交于G,H两点(点G在点M,H之间).(Ⅰ)求椭圆C的方程;(Ⅱ)设直线
与椭圆C交于G,H两点(点G在点M,H之间).(Ⅰ)求椭圆C的方程;(Ⅱ)设直线![]() 的斜率
的斜率![]() ,在x轴上是否存在点P(
,在x轴上是否存在点P(![]() ,0),使得以PG,PH为邻边的平行四边形是菱形?如果存在,求出
,0),使得以PG,PH为邻边的平行四边形是菱形?如果存在,求出![]() 的取值范围;如果不存在,请说明理由;(Ⅲ)若实数
的取值范围;如果不存在,请说明理由;(Ⅲ)若实数![]() 满足
满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新中国成立70周年,社会各界以多种形式的庆祝活动祝福祖国,其中,“快闪”因其独特新颖的传播方式吸引大众眼球.根据腾讯指数大数据,关注“快闪”系列活动的网民群体年龄比例构成,及男女比例构成如图所示,则下面相关结论中不正确的是( )
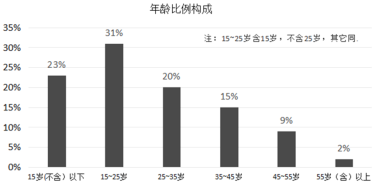
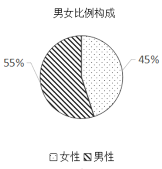
A.35岁以下网民群体超过70%
B.男性网民人数多于女性网民人数
C.该网民群体年龄的中位数在15~25之间
D.25~35岁网民中的女性人数一定比35~45岁网民中的男性人数多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述中正确的是( )
A.若a,b,c∈R,且a>c,则“ab2>cb2”
B.命题“对任意x∈R,有x2≥0”的否定是“存在x∈R,有x2≤0”
C.“![]() ”是“y=sin(2x+φ)为偶函数”的充要条件
”是“y=sin(2x+φ)为偶函数”的充要条件
D.![]() 是一条直线,α,β是两个不同的平面,若l⊥α,l⊥β,则α∥β
是一条直线,α,β是两个不同的平面,若l⊥α,l⊥β,则α∥β
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某气象站统计了4月份甲、乙两地的天气温度(单位![]() ),统计数据的茎叶图如图所示,
),统计数据的茎叶图如图所示,
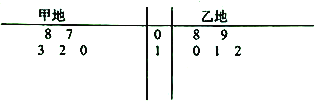
(1)根据所给茎叶图利用平均值和方差的知识分析甲,乙两地气温的稳定性;
(2)气象主管部门要从甲、乙两地各随机抽取一天的天气温度,若甲、乙两地的温度之和大于或等于![]() ,则被称为“甲、乙两地往来温度适宜天气”,求“甲、乙两地往来温度适宜天气”的概率.
,则被称为“甲、乙两地往来温度适宜天气”,求“甲、乙两地往来温度适宜天气”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com