
【题目】设函数f(x)=sin(ωx+φ)![]() cos(ωx+φ)(ω>0,|φ|
cos(ωx+φ)(ω>0,|φ|![]() )的图象与直线y=2的两个相邻的交点之间的距离为π,且f(x)+f(﹣x)=0,若g(x)=sin(ωx+φ),则( )
)的图象与直线y=2的两个相邻的交点之间的距离为π,且f(x)+f(﹣x)=0,若g(x)=sin(ωx+φ),则( )
A.g(x)在(0,![]() )上单调递增B.g(x)在 (0,
)上单调递增B.g(x)在 (0,![]() )上单调递减
)上单调递减
C.g(x)在(![]() ,
,![]() )上单调递增D.g(x)在(
)上单调递增D.g(x)在(![]() ,
,![]() )上单调递减
)上单调递减
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】定义域是一切实数的函数![]() ,其图象是连续不断的,且存在常数
,其图象是连续不断的,且存在常数![]() (
(![]() )使得
)使得![]() 对任意实数
对任意实数![]() 都成立,则称
都成立,则称![]() 是一个“
是一个“![]() -伴随函数”,有下列关于“
-伴随函数”,有下列关于“![]() -伴随函数”的结论:①
-伴随函数”的结论:①![]() 是常数函数唯一一个“
是常数函数唯一一个“![]() -伴随函数”;②“
-伴随函数”;②“![]() -伴随函数”至少有一个零点;③
-伴随函数”至少有一个零点;③![]() 是一个“
是一个“![]() -伴随函数”;其中正确结论的个数( )
-伴随函数”;其中正确结论的个数( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果存在实常数a和b,使得函数![]() 总满足
总满足![]() ,我们称这样的函数
,我们称这样的函数![]() 是“
是“![]() 型函数”.请解答以下问题:
型函数”.请解答以下问题:
(1)已知函数![]() 是“
是“![]() 型函数”,求p和b的值;
型函数”,求p和b的值;
(2)已知函数![]() 是“
是“![]() 型函数”,求一组满足条件的k、m和a的值,并说明理由.
型函数”,求一组满足条件的k、m和a的值,并说明理由.
(3)已知函数![]() 是一个“
是一个“![]() 型函数”,且
型函数”,且![]() ,
,![]() 是增函数,若
是增函数,若![]() 是
是![]() 在区间
在区间![]() 上的图像上的点,求点M随着
上的图像上的点,求点M随着![]() 变化可能到达的区域的面积的大小,并证明你的结论.
变化可能到达的区域的面积的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某高中学生的体能测试结果中,随机抽取100名学生的测试结果,按体重分组得到如图所示的频率分布直方图.
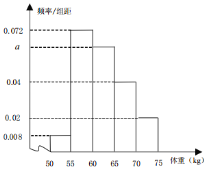
(1)若该校约有![]() 的学生体重不超过“标准体重
的学生体重不超过“标准体重![]() ”,试估计
”,试估计![]() 的值,并说明理由;
的值,并说明理由;
(2)从第3、4、5组中用分层抽样的方法抽取6名学生进行了第二次测试,现从这6人中随机抽取2人进行日常运动习惯的问卷调查,求抽到4组的人数![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬中华优秀传统文化,某中学高三年级利用课余时间组织学生开展小型知识竞赛.比赛规则:每个参赛者回答A、B两组题目,每组题目各有两道题,每道题答对得1分,答错得0分,两组题目得分的和做为该选手的比赛成绩.小明估计答对A组每道题的概率均为![]() ,答对B组每道题的概率均为
,答对B组每道题的概率均为![]() .
.
(Ⅰ)按此估计求小明A组题得分比B组题得分多1分的概率;
(Ⅱ)记小明在比赛中的得分为ξ,按此估计ξ的分布列和数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的一个焦点为
的一个焦点为![]() ,四条直线
,四条直线![]() ,
,![]() 所围成的区域面积为
所围成的区域面积为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设过![]() 的直线
的直线![]() 与
与![]() 交于不同的两点
交于不同的两点![]() ,设弦
,设弦![]() 的中点为
的中点为![]() ,且
,且![]() (
(![]() 为原点),求直线
为原点),求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为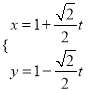 (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的极坐标方程为
的极坐标方程为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() ,
, ![]() 两点,
两点, ![]() 点的直角坐标为
点的直角坐标为![]() .
.
(Ⅰ)将直线![]() 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com