
| A. | $\frac{7}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 作出平面区域Ω和单位圆x2+y2=1,数形结合可得当P到原点距离最小时,△PAB的面积最小,由三角形的知识可得.
解答 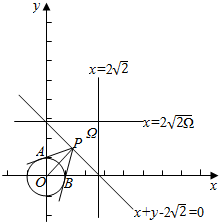 解:作出平面区域Ω和单位圆x2+y2=1,l:x+y-2$\sqrt{2}$=0,
解:作出平面区域Ω和单位圆x2+y2=1,l:x+y-2$\sqrt{2}$=0,
数形结合可得SPABO=2S△PAO=2×$\frac{1}{2}$×PA×1=PA,
设PA=x,△ABO的面积为$\frac{1}{2}$sin∠AOB=$\frac{1}{2}$•$\frac{2x}{1+{x}^{2}}$=$\frac{x}{1+{x}^{2}}$,
即有△PAB的面积为x-$\frac{x}{1+{x}^{2}}$=$\frac{{x}^{3}}{1+{x}^{2}}$,由于在X>0上递增,
∴当P到原点距离最小时,PA最小,△PAB的面积最小,
此时PO⊥l,且|PO|=2,故∠PAO=$\frac{π}{6}$,
∴∠APB=$\frac{π}{3}$,cos∠APB=$\frac{1}{2}$,
故选:B.
点评 本题考查简单线性规划,准确作图并转化是解决问题的关键,属中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:2:3 | B. | 3:2:1 | C. | 2:$\sqrt{3}$:1 | D. | 1:$\sqrt{3}$:2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,$\sqrt{3}$)三点,连接AB,过点B作BC∥x轴交该抛物线于点C.
如图,已知抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,$\sqrt{3}$)三点,连接AB,过点B作BC∥x轴交该抛物线于点C.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com