

分析 由已知可得$\overrightarrow{CD}$=$\overrightarrow{CA}$+$\overrightarrow{AB}$+$\overrightarrow{BD}$,利用数量积的性质即可得出.
解答  解:∵CA⊥AB,∴$\overrightarrow{CA}$•$\overrightarrow{AB}$=0,
解:∵CA⊥AB,∴$\overrightarrow{CA}$•$\overrightarrow{AB}$=0,
∵线段AC⊥α,∴$\overrightarrow{AC}$•$\overrightarrow{BD}$=0
∵BD⊥AB,∴$\overrightarrow{AB}$$•\overrightarrow{BD}$=0.
∵$\overrightarrow{CD}$=$\overrightarrow{CA}$+$\overrightarrow{AB}$+$\overrightarrow{BD}$,AB=a,BD=b,Ac=c,
∴$\overrightarrow{CD}$2=($\overrightarrow{CA}$+$\overrightarrow{AB}$+$\overrightarrow{BD}$)2=a2+b2+c2+0+0+0
∴|$\overrightarrow{CD}$|=$\sqrt{{a}^{2}+{b}^{2}+{c}^{2}}$.
∴C、D间的距离为$\sqrt{{a}^{2}+{b}^{2}+{c}^{2}}$.
点评 本题考查空间两点间的距离的求法,熟练掌握向量的运算和数量积运算是解题的关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:解答题
 已知四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD.异面直线PB与CD所成的角为45°.求:
已知四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD.异面直线PB与CD所成的角为45°.求:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
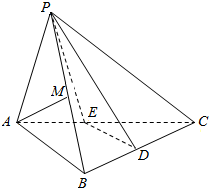 如图,三棱锥P-ABC中,BC⊥平面PAB.PA=PB=AB=BC=6,点M,N分别为PB,BC的中点.
如图,三棱锥P-ABC中,BC⊥平面PAB.PA=PB=AB=BC=6,点M,N分别为PB,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组(分数) | 频数 | 频率 |
| [60,70) | 0.12 | |
| [70,80) | 20 | |
| [80,90) | 0.24 | |
| [90,100] | 12 | |
| 合计 | 50 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com