
【题目】定义在R上的奇函数f(x),当x≥0时,f(x)= ,则关于x的函数F(x)=f(x)-
,则关于x的函数F(x)=f(x)-![]() 的所有零点之和为______.
的所有零点之和为______.
【答案】![]()
【解析】
根据分段函数的解析式和奇函数的对称性作出函数![]() 在
在![]() 上的图象和
上的图象和![]() 的图象,利用数形结合的方法求解即可
的图象,利用数形结合的方法求解即可
∵当x≥0时,f(x)=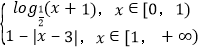 ;
;
即x∈![]() 时,f(x)=
时,f(x)=![]()
x∈[1,3]时,f(x)=x-2∈[-1,1];
x∈(3,+∞)时,f(x)=4-x∈(-∞,-1)
画出x≥0时f(x)的图象,
再利用奇函数的对称性,画出x<0时f(x)的图象,如图所示;
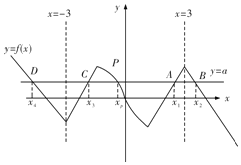
则直线![]() ,与y=f(x)的图象有5个交点,则方程f(x)-
,与y=f(x)的图象有5个交点,则方程f(x)-![]() =0共五个实根,
=0共五个实根,
最左边两根之和为-6,最右边两根之和为6,
∵x∈(-1,0)时,-x∈(0,1),∴f(-x)=![]()
又f(-x)=-f(x),
∴f(x)=-![]() =
=![]()
∴中间的一个根满足![]()
即1-x=![]() ,解得x=1-
,解得x=1-![]() ,
,
∴所有根的和为![]()
故答案为:![]()


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (x∈(-1,1)),有下列结论:
(x∈(-1,1)),有下列结论:
(1)x∈(-1,1),等式f(-x)+f(x)=0恒成立;
(2)m∈[0,+∞),方程|f(x)|=m有两个不等实数根;
(3)x1,x2∈(-1,1),若x1≠x2,则一定有f(x1)≠f(x2);
(4)存在无数多个实数k,使得函数g(x)=f(x)-kx在(-1,1)上有三个零点
则其中正确结论的序号为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项等比数列{an}的前n项和为Sn , 且S2=6,S4=30,n∈N* , 数列{bn}满足bnbn+1=an , b1=1
(1)求an , bn;
(2)求数列{bn}的前n项和为Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,C是以AB为直径的圆O上异于A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F 分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l. 
(Ⅰ)求证:直线l⊥平面PAC;
(Ⅱ)直线l上是否存在点Q,使直线PQ分别与平面AEF、直线EF所成的角互余?若存在,求出|AQ|的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的奇数项成等差数列,偶数项成等比数列,且公差和公比都是2,若对满足m+n≤5的任意正整数m,n,均有am+an=am+n成立. (I)求数列{an}的通项公式;
(II)若bn=  ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com