
【题目】下列说法正确的是( )
A.二进制数11010(2)化为八进制数为42(8)
B.若扇形圆心角为2弧度,且扇形弧所对的弦长为2,则这个扇形的面积为 ![]()
C.用秦九韶算法计算多项式f(x)=3x6+5x4+6x3﹣4x﹣5当x=3时的值时,v1=3v0+5=32
D.正切函数在定义域内为单调增函数
【答案】B
【解析】解:A.二进制数11010(2)=1×24+1×23+0×22+1×21+0×20=26.
∵26÷8=3…2
3÷8=0…3
∴26(10)=32(8)故A错误,
B.如图:设∠AOB=2,AB=2,过点0作OC⊥AB,C为垂足,
并延长OC交 ![]() 于D,则∠AOD=∠BOD=1,AC=
于D,则∠AOD=∠BOD=1,AC= ![]() AB=1.
AB=1.
Rt△AOC中,r=AO= ![]() =
= ![]() ,
,
从而弧长为l=αr=2× ![]() =
= ![]() ,
,
则这个扇形的面积为S= ![]() =
= ![]() ,故B正确,
,故B正确,
C.由秦九韶算法可得f(x)=(((((3x+5)x+6)x+0)x﹣4)x﹣5),
当x=3时,可得v0=3,v1=2﹣12=﹣10,v2=﹣10×2+60=40,v3=40×2﹣160=﹣80.
v0=a6=3,v1=v0x+a5=3×3+5=14,故C错误,
D.正切函数在每一个区间内(kπ﹣ ![]() ,kπ+﹣
,kπ+﹣ ![]() )为单调增函数,但在定义域内不是单调函数,故D错误,
)为单调增函数,但在定义域内不是单调函数,故D错误,
故选:B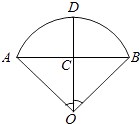
【考点精析】利用命题的真假判断与应用对题目进行判断即可得到答案,需要熟知两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:
【题目】已知A(3,5),B(-1,3),C(-3,1)为△ABC的三个顶点,O、M、N分别为边AB、BC、CA的中点,求△OMN的外接圆的方程,并求这个圆的圆心和半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【河南省2017届高中毕业年级考前预测数学(理)】已知圆![]() 与直线
与直线![]() 相切,设点
相切,设点![]() 为圆上一动点,
为圆上一动点, ![]() 轴于
轴于![]() ,且动点
,且动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)直线![]() 与直线
与直线![]() 垂直且与曲线
垂直且与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2015江苏高考,18】如图,在平面直角坐标系xOy中,已知椭圆![]() 的离心率为
的离心率为![]() ,且右焦点F到左准线l的距离为3.
,且右焦点F到左准线l的距离为3.
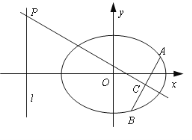
(1)求椭圆的标准方程;
(2)过F的直线与椭圆交于A,B两点,线段AB的垂直平分线分别交直线l和AB于点P,C,若PC=2AB,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区拟建立一个艺术博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从![]() 个招标问题中随机抽取
个招标问题中随机抽取![]() 个问题,已知这
个问题,已知这![]() 个招标问题中,甲公司可正确回答其中的
个招标问题中,甲公司可正确回答其中的![]() 道題目,而乙公司能正确回答毎道题目的概率均为
道題目,而乙公司能正确回答毎道题目的概率均为![]() ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
(1)求甲、乙两家公司共答对![]() 道题目的概率;
道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在D上的函数,若存在区间[m,n]D及正实数k,使函数f(x)在[m,n]上的值域恰为[km,kn],则称函数f(x)是k型函数.给出下列说法:
①f(x)=3﹣ ![]() 不可能是k型函数;
不可能是k型函数;
②若函数f(x)= ![]() (a≠0)是1型函数,则n﹣m的最大值为
(a≠0)是1型函数,则n﹣m的最大值为 ![]() ;
;
③若函数f(x)=﹣ ![]() x2+x是3型函数,则m=﹣4,n=0.
x2+x是3型函数,则m=﹣4,n=0.
其中正确说法个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos2ωx﹣sin2ωx+2 ![]() cosωxsinωx,其中ω>0,若f(x)相邻两条对称轴间的距离不小于
cosωxsinωx,其中ω>0,若f(x)相邻两条对称轴间的距离不小于 ![]()
(1)求ω的取值范围及函数f(x)的单调递增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,a= ![]() ,b+c=3,当ω最大时,f(A)=1,求sinBsinC的值.
,b+c=3,当ω最大时,f(A)=1,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市对贫困家庭自主创业给予小额贷款补贴,每户贷款额为![]() 万元,贷款期限有
万元,贷款期限有![]() 个月、
个月、![]() 个月、
个月、![]() 个月、
个月、![]() 个月、
个月、![]() 个月五种,这五种贷款期限政府分别需要补助
个月五种,这五种贷款期限政府分别需要补助![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元,从
元,从![]() 年享受此项政策的困难户中抽取了
年享受此项政策的困难户中抽取了![]() 户进行了调查统计,选取贷款期限的频数如下表:
户进行了调查统计,选取贷款期限的频数如下表:
贷款期限 |
|
|
|
|
|
频数 |
|
|
|
|
|
以商标各种贷款期限的频率作为![]() 年贫困家庭选择各种贷款期限的概率.
年贫困家庭选择各种贷款期限的概率.
(1)某小区![]() 年共有
年共有![]() 户准备享受此项政策,计算其中恰有两户选择贷款期限为
户准备享受此项政策,计算其中恰有两户选择贷款期限为![]() 个月的概率;
个月的概率;
(2)设给享受此项政策的某困难户补贴为![]() 元,写出
元,写出![]() 的分布列,若预计
的分布列,若预计![]() 年全市有
年全市有![]() 万户享受此项政策,估计
万户享受此项政策,估计![]() 年该市共要补贴多少万元.
年该市共要补贴多少万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com