
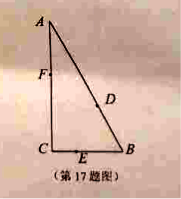
����Ŀ����2017��һģ����ͼ��ij���������۹���![]() Χ��ֱ�������Σ�����ֱ�DZ�
Χ��ֱ�������Σ�����ֱ�DZ�![]() ��
��
б��![]() �����мס��ҡ�����λС���ѷֱ���
�����мס��ҡ�����λС���ѷֱ���![]() �������Ϸ������λ
�������Ϸ������λ
�÷ֱ��Ϊ��![]() ��
��
��1�������Ҷ���ÿ����![]() ���ٶȴӵ�
���ٶȴӵ�![]() �����ڸ��ԵĴ���ϱ��ߣ����������һ��
�����ڸ��ԵĴ���ϱ��ߣ����������һ��
ʱ��ͣ���ұȼ׳�![]() ���ӳ��������ҳ���
���ӳ��������ҳ���![]() ���Ӻ����ʱ��������֮��ľ��룻
���Ӻ����ʱ��������֮��ľ��룻
��2����![]() ���ұ�֮��ľ����Ǽ���֮������
���ұ�֮��ľ����Ǽ���֮������![]() ������
������![]() ���뽫��
���뽫��
��֮��ľ���![]() ��ʾΪ
��ʾΪ![]() �ĺ������������֮�����С������
�ĺ������������֮�����С������
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017���ϳ�ɳ��ģ����֪����![]() ��
��![]() .
.
��1��֤����![]() ��ֱ��
��ֱ��![]() ����������
����������![]() �����ߣ�
�����ߣ�
��2����![]() ��ʹ
��ʹ![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������������ڵ�ֱ�߷��̷ֱ�Ϊx+2y��5=0��y��2=0��x+y��4=0�����ܹ����Ǵ��������������С��Բ�ķ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD��A1B1C1D1�У�����P�ڵ���ABCD�ڣ���P����AD�ľ����뵽��Խ���BC1�ľ�����ȣ����P�Ĺ켣�ǣ�������
A.�߶�
B.��Բ��һ����
C.˫���ߵ�һ����
D.�����ߵ�һ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ձ�����2016-2017ѧ��ȸ����꼶��һѧ����ĩ��������ͼ����֪![]() ����ֱ�λ�ڶ�������
����ֱ�λ�ڶ�������![]() ��
��![]() ���ͺ���С����
���ͺ���С����![]() ������
������![]() ��
��![]() ��
��
��������![]() ����
����![]() ���ּƻ�����һ��������ͨ
���ּƻ�����һ��������ͨ![]() ������
������
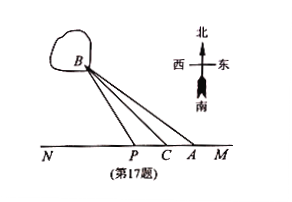
�������跽���������߶�![]() ��ˮ�����裻���ں���
��ˮ�����裻���ں���![]() ��ѡһ��
��ѡһ��![]() �������߶�
�������߶�![]() �ڵ�
�ڵ�
�����裬�����߶�![]() ��ˮ�����裬Ԥ����¡�ˮ�µĵ���������÷ֱ�Ϊ
��ˮ�����裬Ԥ����¡�ˮ�µĵ���������÷ֱ�Ϊ![]() ��Ԫ�M
��Ԫ�M![]() ��
��
![]() ��Ԫ�M
��Ԫ�M![]() ��
��
��1����![]() �����ľ��룻
�����ľ��룻
��2��Ӧ��������裬ʹ�����������ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017������«���ж�ģ����֪����![]() ���㣺
���㣺 ![]() .
.
��1��������![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2����![]() ,������
,������![]() ��ǰ
��ǰ![]() ���
���![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������{an}��ǰ���ΪSn �� ��Sn= ![]() ��{bn}Ϊ�Ȳ����У���a1=b1 �� a2��b2��b1��=a1 ��
��{bn}Ϊ�Ȳ����У���a1=b1 �� a2��b2��b1��=a1 ��
��1��������{an}��{bn}ͨ�ʽ��
��2���� ![]() ��������{cn}��ǰn���Tn ��
��������{cn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C���Եı߷ֱ���a��b��c��������csinA�� ![]() acosC=0��
acosC=0��
��1�����C�Ĵ�С��
��2����c=2�����ABC�����S�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017���ջ�����ģ��ѡ��4��4������ϵ���������
��ֱ������ϵ![]() ��, ��
��, ��![]() ����,
Ϊ����, ![]() ��������Ϊ���Ὠ��������ϵ, Բ
��������Ϊ���Ὠ��������ϵ, Բ![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ,ֱ��
,ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ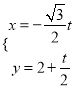 ��tΪ�������� ֱ��
��tΪ�������� ֱ��![]() ��Բ
��Բ![]() ����
����![]() ���㡣
���㡣
������Բ�ĵļ����ꣻ
����ֱ��![]() ��
��![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com