
分析 (1)由题意设z=x+yi(x,y∈R且y≠0),由复数的模和条件列出方程化简即可;
(2)先化简$\frac{z}{m}+\frac{m}{z}$整理出实部、虚部,根据实数的充要条件列出方程,结合题意和(1)的结论求出m的值;
(3)化简(1-2i)z整理出实部、虚部,根据条件列出关系式,代入|z|对应的方程求出x、y,即可求出复数z.
解答 解:(1)设z=x+yi(x,y∈R且y≠0),
由|2z+5|=|z+10|得:(2x+5)2+4y2=(x+10)2+y2
化简得:x2+y2=25,所以|z|=5.…(4分)
(2)∵$\frac{z}{m}+\frac{m}{z}=(\frac{x}{m}+\frac{mx}{{{m^2}+{n^2}}})+(\frac{y}{m}-\frac{my}{{{x^2}+{y^2}}})i∈R$,
∴$\frac{y}{m}-\frac{my}{{{x^2}+{y^2}}}=0$,
又y≠0且m2 +n2=25,∴$\frac{1}{m}-\frac{m}{25}=0$,解得m=±5.…(8分)
(3)由(1-2i)z=(1-2i)(x+yi)=(x+2y)+(y-2x)i及已知得:x+2y=y-2x,
即y=-3x,代入x2+y2=25解得:$\left\{\begin{array}{l}x=\frac{{\sqrt{10}}}{2}\\ y=-\frac{{3\sqrt{10}}}{2}\end{array}\right.$或$\left\{\begin{array}{l}x=-\frac{{\sqrt{10}}}{2}\\ y=\frac{{3\sqrt{10}}}{2}\end{array}\right.$,
故$z=\frac{{\sqrt{10}}}{2}-\frac{{3\sqrt{10}}}{2}i$或$z=-\frac{{\sqrt{10}}}{2}+\frac{{3\sqrt{10}}}{2}i$.…(14分)
点评 本题考查复数代数形式的混合运算,复数的模,以及复数的基本概念,考查方程思想,化简、计算能力.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{ab}>\frac{1}{2}$ | B. | a2+b2≥8 | C. | $\sqrt{ab}$≥2 | D. | $\frac{1}{a}+\frac{1}{b}$≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
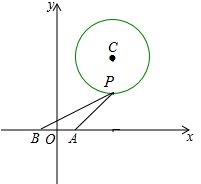 如图,在平面直角坐标系内,已知A(1,0),B(-1,0)两点,且圆C的方程为x2+y2-6x-8y+21=0,点P为圆C上的动点.
如图,在平面直角坐标系内,已知A(1,0),B(-1,0)两点,且圆C的方程为x2+y2-6x-8y+21=0,点P为圆C上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {0,1} | C. | {0} | D. | {-1,0} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com