
如图所示,四边形EFGH所在平面为三棱锥A-BCD的一个截面,四边形EFGH为平行四边形.
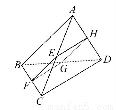
(1)求证:AB∥平面EFGH,CD∥平面EFGH.
(2)若AB=4,CD=6,求四边形EFGH周长的取值范围.
(1)见解析 (2) (8,12)
【解析】(1)∵四边形EFGH为平行四边形,
∴EF∥GH.
∵HG?平面ABD,EF?平面ABD,
∴EF∥平面ABD.
∵EF?平面ABC,平面ABD∩平面ABC=AB,
∴EF∥AB.
∵EF?平面EFGH,AB?平面EFGH,
∴AB∥平面EFGH.
同理可得CD∥平面EFGH.
(2)设EF=x(0<x<4),四边形EFGH的周长为l.
由(1)知EF∥AB,则 =
= .
.
又由(1)同理可得CD∥FG,
则 =
= ,
,
∴ =
= =
=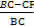 =1-
=1- .
.
从而FG=6-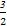 x.
x.
∴四边形EFGH的周长l=2(x+6-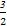 x)=12-x.
x)=12-x.
又0<x<4,∴8<l<12,
即四边形EFGH周长的取值范围为(8,12).


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(七)第二章第四节练习卷(解析版) 题型:选择题
函数y=|2x-1|在区间(k-1,k+1)内不单调,则k的取值范围是( )
(A)(-1,+∞) (B)(-∞,1)
(C)(-1,1) (D)(0,2)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十六第七章第五节练习卷(解析版) 题型:选择题
已知两条直线m,n,两个平面α,β,给出下面四个命题:
①m∥n,m⊥α⇒n⊥α;
②α∥β,m?α,n?β⇒m∥n;
③m∥n,m∥α⇒n∥α;
④α∥β,m∥n,m⊥α⇒n⊥β.
其中正确命题的序号是( )
(A)①③ (B)②④ (C)①④ (D)②③
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十八第七章第七节练习卷(解析版) 题型:填空题
在正方体ABCD-A1B1C1D1中,若E是A1C1的中点,则直线CE与BD的位置关系是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十八第七章第七节练习卷(解析版) 题型:选择题
若直线l⊥平面α,直线l的方向向量为s,平面α的法向量为n,则下列结论正确的是( )
(A)s=(1,0,1),n=(1,0,-1)
(B)s=(1,1,1),n=(1,1,-2)
(C)s=(2,1,1),n=(-4,-2,-2)
(D)s=(1,3,1),n=(2,0,-1)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十五第七章第四节练习卷(解析版) 题型:填空题
设互不相同的直线l,m,n和平面α,β,γ,给出下列三个命题:
①若l与m为异面直线,l?α,m?β,则α∥β;
②若α∥β,l?α,m?β,则l∥m;
③若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.
其中真命题的个数为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十五第七章第四节练习卷(解析版) 题型:选择题
已知直线m,n和平面α,则m∥n的一个必要不充分条件是( )
(A)m∥α,n∥α (B)m⊥α,n⊥α
(C)m∥α,n?α (D)m,n与α成等角
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十九第七章第八节练习卷(解析版) 题型:解答题
如图,已知正四棱锥P-ABCD的所有棱长都是2,底面正方形两条对角线相交于O点,M是侧棱PC的中点.
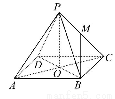
(1)求此正四棱锥的体积.
(2)求直线BM与侧面PAB所成角θ的正弦值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十七第七章第六节练习卷(解析版) 题型:选择题
已知正方体ABCD-A1B1C1D1中,点E为上底面A1C1的中心,若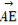 =
=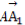 +x
+x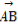 +y
+y ,则x,y的值分别为( )
,则x,y的值分别为( )
(A)x=1,y=1 (B)x=1,y=
(C)x= ,y=
,y= (D)x=
(D)x= ,y=1
,y=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com