
【题目】![]() 是边长为
是边长为![]() 的等边三角形,E、F分别为AB、AC的中点,
的等边三角形,E、F分别为AB、AC的中点,![]() ,沿EF把
,沿EF把![]() 折起,使点A翻折到点P的位置,连接PB、PC,则四棱锥
折起,使点A翻折到点P的位置,连接PB、PC,则四棱锥![]() 的外接球的表面积的最小值为________,此时四棱锥
的外接球的表面积的最小值为________,此时四棱锥![]() 的体积为________.
的体积为________.
【答案】![]()
![]()
【解析】
根据题意,当梯形BCEF的外接圆的圆心为四棱锥的外接球的球心时,外接球的半径最小,易得BC的中点即为梯形的外接圆圆心,也即为四棱锥![]() 的球心,进而求解.
的球心,进而求解.
如图所示:
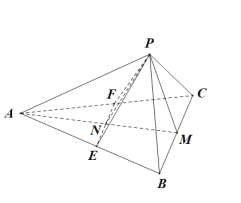
四边形BCEF为梯形,则必有外接圆,设O为梯形BCEF的外接圆的圆心,即为外接球的球心时,外接球的半径最小,也就使得外接球的表面积最小,过A作BC的垂线交BC于点M,交EF于点N,连接PM,PN,点O必在AM上,
因为E,F,分别为中点,
所以![]() ,
,
所以![]() ,即
,即![]() 是直角三角形,
是直角三角形,
因为![]() 是边长为
是边长为![]() 的等边三角形,E、F分别为AB、AC的中点,
的等边三角形,E、F分别为AB、AC的中点,
所以![]() ,
,
所以点M为为梯形BCEF的外接圆的圆心,即点O与点M重合,
所以![]() ,
,![]() ,
,
所以四棱锥![]() 的高为:
的高为:![]() ,
,
所以棱锥![]() 的外接球的表面积的最小值为
的外接球的表面积的最小值为![]() ,
,
此时四棱锥![]() 的体积为
的体积为![]() .
.
故答案为:(1). ![]() (2).
(2). ![]()


科目:高中数学 来源: 题型:
【题目】某市为提升中学生的数学素养,激发学生学习数学的兴趣,举办了一次“数学文化知识大赛”,分预赛和复赛两个环节.已知共有8000名学生参加了预赛,现从参加预赛的全体学生中随机地抽取100人的预赛成绩作为样本,得到如下频率分布直方图.
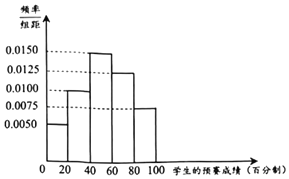
(1)规定预赛成绩不低于80分为优良,若从上述样本中预赛成绩不低于60分的学生中随机地抽取2人,求恰有1人预赛成绩优良的概率;
(2)由频率分布直方图可认为该市全体参加预赛学生的预赛成绩Z服从正态分布N(μ,σ2),其中μ可近似为样本中的100名学生预赛成绩的平均值(同一组数据用该组区间的中点值代替),且σ2=362.利用该正态分布,估计全市参加预赛的全体学生中预赛成绩不低于91分的人数;
(3)预赛成绩不低于91分的学生将参加复赛,复赛规则如下:①每人的复赛初始分均为100分;②参赛学生可在开始答题前自行决定答题数量n,每一题都需要“花”掉(即减去)一定分数来获取答题资格,规定答第k题时“花”掉的分数为0.1k(k∈(1,2n));③每答对一题加1.5分,答错既不加分也不减分;④答完n题后参赛学生的最终分数即为复赛成绩.已知学生甲答对每道题的概率均为0.7,且每题答对与否都相互独立.若学生甲期望获得最佳的复赛成绩,则他的答题数量n应为多少?
(参考数据:![]() ;若Z~N(μ,σ2),则P(μ﹣σ<Z<μ+σ)≈0.6827,P(μ﹣2σ<Z<μ+2σ)≈0.9545,P(μ﹣3σ<Z<μ+3σ)≈0.9973.
;若Z~N(μ,σ2),则P(μ﹣σ<Z<μ+σ)≈0.6827,P(μ﹣2σ<Z<μ+2σ)≈0.9545,P(μ﹣3σ<Z<μ+3σ)≈0.9973.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2a=2bcosC+csinB.
(Ⅰ)求tanB;
(Ⅱ)若C![]() ,△ABC的面积为6,求BC.
,△ABC的面积为6,求BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为D,若存在实常数
的定义域为D,若存在实常数![]() 及
及![]() ,对任意
,对任意![]() ,当
,当![]() 且
且![]() 时,都有
时,都有![]() 成立,则称函数
成立,则称函数![]() 具有性质
具有性质![]() .
.
(1)判断函数![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)若函数![]() 具有性质
具有性质![]() ,求
,求![]() 及
及![]() 应满足的条件;
应满足的条件;
(3)已知函数![]() 不存在零点,当
不存在零点,当![]() 时具有性质
时具有性质![]() (其中
(其中![]() ,
,![]() ),记
),记![]() ,求证:数列
,求证:数列![]() 为等比数列的充要条件是
为等比数列的充要条件是![]() 或
或![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 为等边三角形,且垂直于底面
为等边三角形,且垂直于底面![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)已知点![]() 在棱
在棱![]() 上且
上且![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+lnx(a∈R).
(1)当a=![]() 时,求f(x)在区间[1,e]上的最大值和最小值;
时,求f(x)在区间[1,e]上的最大值和最小值;
(2)如果函数g(x),f1(x),f2(x),在公共定义域D上,满足f1(x)<g(x)<f2(x),那么就称g(x)为f1(x),f2(x)的“活动函数”.已知函数![]() .
. ![]() 。若在区间(1,+∞)上,函数f(x)是f1(x),f2(x)的“活动函数”,求a的取值范围.
。若在区间(1,+∞)上,函数f(x)是f1(x),f2(x)的“活动函数”,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是正方形,点
是正方形,点![]() 在以
在以![]() 为直径的半圆弧上(
为直径的半圆弧上(![]() 不与
不与![]() ,
,![]() 重合),
重合),![]() 为线段
为线段![]() 的中点,现将正方形
的中点,现将正方形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
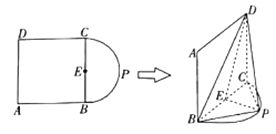
(1)证明:![]() 平面
平面![]() .
.
(2)若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,求
的体积最大时,求![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com