
【题目】如图,在三棱柱![]() 中,侧面
中,侧面![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
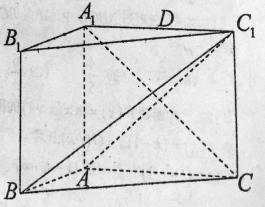
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() 是
是![]() 的中点,判断并证明在线段
的中点,判断并证明在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ,若存在,求点
,若存在,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)![]() 为
为![]() 的中点,
的中点,![]() .
.
【解析】
试题分析:(1)借助题设条件运用面面垂直的判定定理推证;(2)借助题设运用线面平行的判定定理及等积法探求.
试题解析:
(1)在三棱柱![]() 中,侧面
中,侧面![]() 是矩形,
是矩形,
![]()
又![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,
![]() ,又
,又![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ………………………………………6分
………………………………………6分
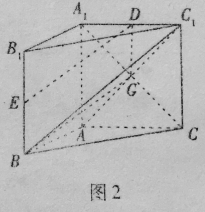
(2)解法一:当![]() 为
为![]() 的中点时,连接
的中点时,连接![]() ,
,
如图1,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
又因为![]() ,
,![]() 平面
平面![]() ,
,
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
![]() ,
,![]() ,
,
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() .…………………………………12分
.…………………………………12分

解法2.当![]() 为
为![]() 的中点时,连接
的中点时,连接![]() ,如图2,设
,如图2,设![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
![]() 且
且![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,则
为平行四边形,则![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ,
,
求距离同解法一.


科目:高中数学 来源: 题型:
【题目】若<<0,则下列不等式:①<;②|a|+b>0;③a->b-;④lna2>lnb2中,正确的是( )
(A)①④ (B)②③ (C)①③ (D)②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球![]() 个.若从袋子中随机抽取1个小球,取到标号为2的小球的概率是
个.若从袋子中随机抽取1个小球,取到标号为2的小球的概率是![]() .
.
(1)求![]() 的值;
的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为![]() ,第二次取出的小球标号为
,第二次取出的小球标号为![]() .
.
(i)记“![]() ”为事件
”为事件![]() ,求事件
,求事件![]() 的概率;
的概率;
(ii)在区间![]() 内任取2个实数
内任取2个实数![]() ,求事件“
,求事件“![]() 恒成立”的概率.
恒成立”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的方程为:
的方程为:![]() ,其中:
,其中:![]() ,且
,且![]() 为常数.
为常数.
(1)判断曲线![]() 的形状,并说明理由;
的形状,并说明理由;
(2)设曲线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于点
轴交于点![]() (
(![]() 不同于坐标原点
不同于坐标原点![]() ),试判断
),试判断![]() 的面积
的面积![]() 是否为定值?并证明你的判断;
是否为定值?并证明你的判断;
(3)设直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,且
,且![]() 为坐标原点),求曲线
为坐标原点),求曲线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个,生产一个卫兵需5分钟,生产一个骑兵需7分钟,生产一个伞兵需4分钟,已知总生产时间不超过10小时,若生产一个卫兵可获利润5元,生产一个骑兵可获利润6元,生产一个伞兵可获利润3元.
(1)用每天生产的卫兵个数![]() 与骑兵个数
与骑兵个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】连江一中第49届田径运动会提出了“我运动、我阳光、我健康、我快乐”的口号,某同学要设计一张如图所示的竖向张贴的长方形海报进行宣传,要求版心面积为162 ![]() (版心是指图中的长方形阴影部分,
(版心是指图中的长方形阴影部分,![]() 为长度单位分米),上、下两边各空2
为长度单位分米),上、下两边各空2 ![]() ,左、右两边各空1
,左、右两边各空1 ![]() .
.

(1)若设版心的高为![]()
![]() ,求海报四周空白面积关于
,求海报四周空白面积关于![]() 的函数
的函数![]() 的解析式;
的解析式;
(2)要使海报四周空白面积最小,版心的高和宽该如何设计?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F并且经过点A(1,﹣2).
(1)求抛物线C的方程;
(2)过F作倾斜角为45°的直线l,交抛物线C于M,N两点,O为坐标原点,求△OMN的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com