①③
分析:①根据f(x-2)=-f(x)对一切x∈R都成立可得f(x+4)=-f(x+2)=f(x);
②设x∈[1,3],则x-2∈[-1,1],根据x∈[-1,1]时,f(x)=x
3,可得f(x-2)=( x-2)
3,从而可得f(x)=-( x-2)
3;
③∵函数y=f(x)是定义在R上的奇函数,且f(x-2)=-f(x),可得f(x-2)=f(-x),从而直线x=-1是函数y=f(x)图象的对称轴,由于函数为奇函数,所以直线x=1也是函数y=f(x)图象的对称轴;
④根据f(x-2)=-f(x),可得f(x-2)+f(x)=0;
⑤由②知f(x)=-( x-2)
3,求出导函数,从而求出切线斜率与切点的坐标,从而可得切线方程.
解答:①,∵f(x-2)=-f(x)对一切x∈R都成立,∴f(x+2)=-f(x),∴f(x+4)=-f(x+2)=f(x),∴函数y=f(x)是以4为周期的周期函数,故①正确;
②,设x∈[1,3],则x-2∈[-1,1],∵当x∈[-1,1]时,f(x)=x
3,∴f(x-2)=( x-2)
3,∵f(x-2)=-f(x)
∴-f(x)=( x-2)
3,∴f(x)=-( x-2)
3,故②不正确;
③,∵函数y=f(x)是定义在R上的奇函数,且f(x-2)=-f(x),∴f(x-2)=f(-x),∴直线x=-1是函数y=f(x)图象的对称轴,由于函数为奇函数,所以直线x=1也是函数y=f(x)图象的对称轴,故③正确;
④,∵f(x-2)=-f(x),∴f(x-2)+f(x)=0,∴点(1,0)是函数y=f(x)图象的对称中心,故④不正确;
⑤,由②知f(x)=-( x-2)
3,则f′(x)=-3( x-2)
2,∴f′(

)=-3(

-2)
2=-

,又f(

)=

∴函数y=f(x)在点(

,f(

))处的切线方程为
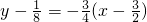
,即3x+4y-5=0,故⑤不正确.
综上知,正确的是①③
故答案为:①③
点评:本题综合考查函数的性质,考查函数的周期性,对称性,考查曲线的切线,涉及知识点多,解题需要谨慎.

 ,f(
,f( ))处的切线方程为3x-y-5=0.
))处的切线方程为3x-y-5=0. )=-3(
)=-3(  -2)2=-
-2)2=- ,又f(
,又f( )=
)=
 ,f(
,f( ))处的切线方程为
))处的切线方程为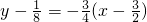 ,即3x+4y-5=0,故⑤不正确.
,即3x+4y-5=0,故⑤不正确.

 阅读快车系列答案
阅读快车系列答案