

| A. | B. | C. | D. |
分析 取AB中点D,连结CD,ED,ED∩AB1=F,连结EF,则C1F即为平面C1 EC 与 AB1 C1 的交线l,以C 为原点,CA为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,利用利用向量法能求出直线l与 AC所成角的余弦值.
解答 解:取AB中点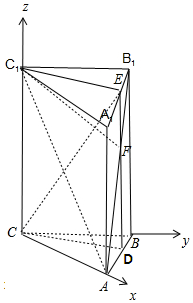 D,连结CD,ED,ED∩AB1=F,连结EF,
D,连结CD,ED,ED∩AB1=F,连结EF,
则C1F即为平面C1 EC 与 AB1 C1 的交线l,
以C 为原点,CA为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,
则A(1,0,0),C(0,0,0),
C1(0,0,2),B1(0,1,2),F(),
=(),=(1,0,0),
设直线l与 AC所成角为θ,
则cosθ===.
∴直线l与 AC所成角的余弦值为.
故选:C.
点评 本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
| A. | 2- | B. | -1 | C. | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
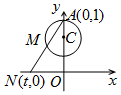 如图,周长为1的圆的圆心C在y轴上,一动点M从圆上的点A(0,1)开始按逆时针方向绕圆运动一周,记走过的弧长为x,直线AM与x轴交于点N(t,0),则函数t=f(x)的图象大致为( )
如图,周长为1的圆的圆心C在y轴上,一动点M从圆上的点A(0,1)开始按逆时针方向绕圆运动一周,记走过的弧长为x,直线AM与x轴交于点N(t,0),则函数t=f(x)的图象大致为( )| A. | 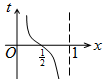 | B. | 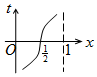 | C. | 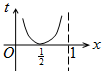 | D. | 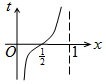 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的图象向左平移π个单位长度可得到y=g(x)的函象 | |
| B. | 函数y=f(x)+g(x)的值域为[-2,2] | |
| C. | 函数y=f(x)•g(x)在上单调递增 | |
| D. | 函数y=f(x)-g(x)的图象关于点对称 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com