
【题目】已知椭圆![]() :
: ![]() 的上下两个焦点分别为
的上下两个焦点分别为![]() ,过点
,过点![]() 与
与![]() 轴垂直的直线交椭圆
轴垂直的直线交椭圆![]() 于
于![]() 两点,
两点, ![]() 的面积为
的面积为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() 为坐标原点,直线
为坐标原点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() 两个不同的点,若
两个不同的点,若![]() ,求
,求![]() 的取值范围.
的取值范围.
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aln(x+1)﹣x2 , 在(1,2)内任取两个实数x1 , x2(x1≠x2),若不等式 ![]() >1恒成立,则实数a的取值范围为( )
>1恒成立,则实数a的取值范围为( )
A.(28,+∞)
B.[15,+∞)
C.[28,+∞)
D.(15,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二八班选出甲、乙、丙三名同学参加级部组织的科学知识竞赛.在该次竞赛中只设成绩优秀和成绩良好两个等次,若某同学成绩优秀,则给予班级10分的班级积分,若成绩良好,则给予班级5分的班级积分.假设甲、乙、丙成绩为优秀的概率分别为 ![]() ,
, ![]() ,
, ![]() ,他们的竞赛成绩相互独立.
,他们的竞赛成绩相互独立.
(1)求在该次竞赛中甲、乙、丙三名同学中至少有一名成绩为优秀的概率;
(2)记在该次竞赛中甲、乙、丙三名同学所得的班级积分之和为随机变量ξ,求随机变量ξ的分布列和数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
(1)求某户居民用电费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(2)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的点80%,求![]() 的值;
的值;
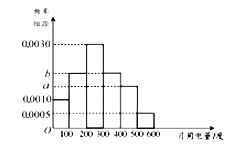
(3)在满足(2)的条件下,估计1月份该市居民用户平均用电费用(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1= ![]() ,且前n项的算术平均数等于第n项的2n﹣1倍(n∈N*).
,且前n项的算术平均数等于第n项的2n﹣1倍(n∈N*).
(1)写出此数列的前5项;
(2)归纳猜想{an}的通项公式,并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的离心率为
)的离心率为![]() ,以原点
,以原点![]() 为圆心,椭圆
为圆心,椭圆![]() 的长半轴长为半径的圆与直线
的长半轴长为半径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)已知点![]() 为动直线
为动直线![]() 与椭圆
与椭圆![]() 的两个交点,问:在
的两个交点,问:在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,试求出点
为定值?若存在,试求出点![]() 的坐标和定值;若不存在,请说明理由.
的坐标和定值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com