
【题目】![]() 年将在日本东京举办第
年将在日本东京举办第![]() 届夏季奥林匹克运动会,简称为“奥运会”,为了解不同年龄的人对“奥运会”的关注程度,某机构随机抽取了年龄在
届夏季奥林匹克运动会,简称为“奥运会”,为了解不同年龄的人对“奥运会”的关注程度,某机构随机抽取了年龄在![]() 岁之间的
岁之间的![]() 人进行调查,经统计,“年轻人”与“中老年人”的人数之比为
人进行调查,经统计,“年轻人”与“中老年人”的人数之比为![]() .
.
关注 | 不关注 | 合计 | |
年轻人 |
| ||
中老年人 | |||
合计 |
|
|
|
(1)根据已知条件完成上面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为是否关注“奥运会”与年龄段有关;
的把握认为是否关注“奥运会”与年龄段有关;
(2)现采用分层抽样的方法从中老年人中选取![]() 人进行问卷调查.若再从这
人进行问卷调查.若再从这![]() 人中选取
人中选取![]() 人进行面对面询问,求事件“选取的
人进行面对面询问,求事件“选取的![]() 人中至少有
人中至少有![]() 人关注奥运会”的概率.
人关注奥运会”的概率.
附参考公式: ,其中
,其中![]() 临界值表:
临界值表:
|
|
|
|
|
|
|
|
 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的方程为
的方程为![]() ,以极点为原点,极轴所在直线为
,以极点为原点,极轴所在直线为![]() 轴建立直角坐标,直线
轴建立直角坐标,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),
为参数),![]() 与
与![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设点![]() ;若
;若![]() 、
、![]() 、
、![]() 成等比数列,求
成等比数列,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明家的晚报在下午![]() 任何一个时间随机地被送到,他们一家人在下午
任何一个时间随机地被送到,他们一家人在下午![]() 任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,
任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,![]() 编号为01,
编号为01,![]() 编号为02,依此类推,
编号为02,依此类推,![]() 编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为
编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为![]()
![]()
7840 1160 5054 3139 8082 7732 5034 3682 4829 4052 |
4201 6277 5678 5188 6854 0200 8650 7584 0136 7655 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构对高三学生的记忆力![]() 和判断力
和判断力![]() 进行统计分析,得下表数据:
进行统计分析,得下表数据:
| 6 | 8 | 10 | 12 |
| 2 | 3 | 5 | 6 |

(1)请在图中画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测记忆力为9的同学的判断力.
相关公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂家具车间造![]() 、
、![]() 型两类桌子,每张桌子需木工和漆工梁道工序完成.已知木工做一张
型两类桌子,每张桌子需木工和漆工梁道工序完成.已知木工做一张![]() 、
、![]() 型型桌子分别需要1小时和2小时,漆工油漆一张
型型桌子分别需要1小时和2小时,漆工油漆一张![]() 、
、![]() 型型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张
型型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张![]() 、
、![]() 型型桌子分别获利润2千元和3千元.
型型桌子分别获利润2千元和3千元.
(1)列出满足生产条件的数学关系式,并画出可行域;
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机支付也称为移动支付,是指允许用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.随着信息技术的发展,手机支付越来越成为人们喜欢的支付方式.某机构对某地区年龄在15到75岁的人群“是否使用手机支付”的情况进行了调查,随机抽取了100人,其年龄频率分布表和使用手机支付的人数如下所示:(年龄单位:岁)
年龄段 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频率 | 0.1 | 0.32 | 0.28 | 0.22 | 0.05 | 0.03 |
使用人数 | 8 | 28 | 24 | 12 | 2 | 1 |
(1)若以45岁为分界点,根据以上统计数据填写下面的2×2列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“使用手机支付”与年龄有关?
年龄低于45岁 | 年龄不低于45岁 | |
使用手机支付 | ||
不使用手机支付 |
(2)若从年龄在[55,65),[65,75]的样本中各随机选取2人进行座谈,记选中的4人中“使用手机支付”的人数为X,求随机变量X的分布列和数学期望.
参考数据:
P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 分别为矩形四条边的中点,以
分别为矩形四条边的中点,以![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() 轴建立直角坐标系(如图所示).若
轴建立直角坐标系(如图所示).若![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上.且
上.且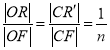 .
.
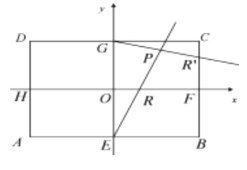
(Ⅰ)求证:直线![]() 与
与![]() 的交点
的交点![]() 总在椭圆
总在椭圆![]() :
:![]() 上;
上;
(Ⅱ)若![]() 、
、![]() 为曲线
为曲线![]() 上两点,且直线
上两点,且直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,求点
,求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() ,点
,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com