
【题目】给出下列4个命题:
①函数![]() 的最小正周期是
的最小正周期是![]() ;②直线
;②直线![]() 是函数
是函数![]() 的一条对称轴;③若
的一条对称轴;③若![]() ,且
,且![]() 为第二象限角,则
为第二象限角,则![]() ;④函数
;④函数![]() 在区间
在区间![]() 上单调递减.其中正确的是__________。(写出所有正确命题的序号)
上单调递减.其中正确的是__________。(写出所有正确命题的序号)
【答案】①②③
【解析】
①根据函数y=![]() 的最小正周期得出函数
的最小正周期得出函数![]() 的最小正周期;
的最小正周期;
②当![]() 时函数y取得最小值,判断
时函数y取得最小值,判断![]() 是函数y的一条对称轴;
是函数y的一条对称轴;
③根据![]() ,且α为第二象限角,求出tanα的值;
,且α为第二象限角,求出tanα的值;
④根据x的取值范围,结合余弦函数的单调性,求出函数y的单调性.
对于①,函数y=![]() 的最小正周期是π,
的最小正周期是π,
∴函数![]() 的最小正周期是
的最小正周期是![]() ,①正确;
,①正确;
对于②,![]() 时,y=2sin(3×
时,y=2sin(3×![]() -
-![]() )=-2为最小值,
)=-2为最小值,
∴直线![]() 是函数
是函数![]() 的一条对称轴,∴②正确;
的一条对称轴,∴②正确;
对于③,若![]() ,则sin2α+2sinαcosα+cos2α=
,则sin2α+2sinαcosα+cos2α=![]() ,
,
∴2sinαcosα=![]() -1=-
-1=-![]() ,
,
又α为第二象限角,∴sinα-cosα>0,![]() ,
,
∴![]() ,③正确;
,③正确;
对于④,x∈![]() 时,2-3x∈(-7,0),
时,2-3x∈(-7,0),
由(-7,0)[-2π,0],
根据余弦函数的图象与性质知,函数y=cos(2-3x)在![]() 上不单调,④错误.
上不单调,④错误.
综上,①②③正确.
故答案为:①②③.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:
【题目】某校举办了一场主题为“爱诗词、爱祖国”的诗词知识竞赛,从参赛的全体学生中抽出30人的成绩作为样本.对这30名学生的成绩进行统计,并按![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分组,得到如图所示的频率分布直方图.
分组,得到如图所示的频率分布直方图.
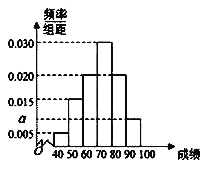
(1)求图中实数![]() 的值;
的值;
(2)估计参加这次知识竞赛的学生的平均成绩及成绩的中位数(平均成绩用每组中点值做代表,结果均保留一位小数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 是圆心为
是圆心为![]() ,半径为1的圆.
,半径为1的圆.
(1)求曲线![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上的点,
上的点, ![]() 为曲线
为曲线![]() 上的点,求
上的点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲船在岛![]() 的正南
的正南![]() 处,以4千米/时的速度向正北方向航行,
处,以4千米/时的速度向正北方向航行,![]() 千米,同时乙船自岛
千米,同时乙船自岛![]() 出发以6千米/时向北偏东60°的方向驶去.当甲、乙两船相距最近时,它们所航行的时间为( )
出发以6千米/时向北偏东60°的方向驶去.当甲、乙两船相距最近时,它们所航行的时间为( )
A.![]() B.
B.![]() C.
C.![]() D.2.15h
D.2.15h
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出三个命题:①直线上有两点到平面的距离相等,则直线平行平面;②夹在两平行平面间的异面直线段的中点的连线平行于这个平面;③过空间一点必有唯一的平面与两异面直线平行.正确的是( )
A. ②③B. ①②C. ①②③D. ②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,
轴的非负半轴为极轴建立极坐标系, ![]() 点的极坐标为
点的极坐标为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)写出点![]() 的直角坐标及曲线
的直角坐标及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 的中点
的中点![]() 到直线
到直线![]() :
: ![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆![]() :
:![]() ,点
,点![]() 是圆
是圆![]() 内一个定点,点
内一个定点,点![]() 是圆上任意一点,线段
是圆上任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和半径
和半径![]() 相交于点
相交于点![]() .当点
.当点![]() 在圆上运动时,点
在圆上运动时,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.

(1)求曲线![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点(点
两点(点![]() 在
在![]() 两点之间).是否存在直线
两点之间).是否存在直线![]() 使得
使得![]() ?若存在,求直线
?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足Sn-n=2(an-2),(n∈N*)
(1)证明:数列{an-1}为等比数列.
(2)若bn=anlog2(an-1),数列{bn}的前项和为Tn,求Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com