
【题目】如图所示,△ABC中,D为AC的中点,AB=2,BC= ![]() ,∠A=
,∠A= ![]() .
. 
(1)求cos∠ABC的值;
(2)求BD的值.
【答案】
(1)解:∵在△ABC中, ![]() ,sinA=
,sinA= ![]() ,
,
∴sinC= ![]() =
= ![]() =
= ![]() ,由BC>AB,可得:A>C,C为锐角,
,由BC>AB,可得:A>C,C为锐角,
∴cosC= ![]() =
= ![]() ,
,
∴cos∠ABC=cos( ![]() ﹣C)=cos
﹣C)=cos ![]() cosC+sin
cosC+sin ![]() sinC=
sinC= ![]()
(2)解:∵AB=2,BC= ![]() ,cos∠ABC=
,cos∠ABC= ![]() .
.
∴在△ABC中,AC2=AB2+BC2﹣2ABBCcos∠ABC=9,可得:AC=3,
∴在△ABD中,BD2=AB2+AD2﹣2AB×ADcosA= ![]() ,
,
∴BD= ![]() .
.
【解析】(1)在△ABC中利用正弦定理可求sinC,利用大边对大角可得C为锐角,利用同角三角函数基本关系式可求cosC,利用两角差的余弦函数公式即可计算得解cos∠ABC的值.(2)由已知在△ABC中,利用余弦定理可求AC,进而在△ABD中,利用余弦定理可求BD.
【考点精析】本题主要考查了余弦定理的定义的相关知识点,需要掌握余弦定理:![]() ;
;![]() ;
;![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】某学生社团在对本校学生学习方法开展问卷调查的过程中发现,在回收上来的1000份有效问卷中,同学们背英语单词的时间安排共有两种:白天背和晚上临睡前背.为研究背单词时间安排对记忆效果的影响,该社团以5%的比例对这1000名学生按时间安排粪型进行分层抽样,并完成一项实验,实验方法是,使两组学生记忆40个无意义音节(如xIQ、GEH),均要求在刚能全部记清时就停止识记,并在8小时后进行记忆测验.不同的是,甲组同学识记结束后一直不睡觉,8小时后测验;乙组同学识记停止后立刻睡觉,8小时后叫醒测验.两组同学识记停止8小时后的准确回忆(保持)情况如图(区间含左端点而不舍右端点) 
(1)估计1000名被调查的学生中识记停止后8小时40个音节的保持率大于等于60%的人数;
(2)从乙组准确回忆结束在|12,24)范围内的学生中随机选3人,记能准确回忆20个以上(含20)的人数为随机变量x.求X分布列及数学期望;
(3)从本次实验的结果来看,上述两种时间安排方法中哪种方法背英语单词记忆效果更好?计算并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 与抛物线y2=2px(p>0)共焦点F2 , 抛物线上的点M到y轴的距离等于|MF2|﹣1,且椭圆与抛物线的交点Q满足|QF2|=
与抛物线y2=2px(p>0)共焦点F2 , 抛物线上的点M到y轴的距离等于|MF2|﹣1,且椭圆与抛物线的交点Q满足|QF2|= ![]() . (Ⅰ)求抛物线的方程和椭圆的方程;
. (Ⅰ)求抛物线的方程和椭圆的方程;
(Ⅱ)过抛物线上的点P作抛物线的切线y=kx+m交椭圆于A、B两点,求此切线在x轴上的截距的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0),离心率为
=1(a>b>0),离心率为 ![]() ,两焦点分别为F1、F2 , 过F1的直线交椭圆C于M,N两点,且△F2MN的周长为8.
,两焦点分别为F1、F2 , 过F1的直线交椭圆C于M,N两点,且△F2MN的周长为8.
(1)求椭圆C的方程;
(2)过点P(m,0)作圆x2+y2=1的切线l交椭圆C于A,B两点,求弦长|AB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年中国(云南赛区)三对三篮球联赛在昆明市体育局的大力支持下,圆满顺利结束.组织方统计了来自 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 球队的男子的平均身高与本次比赛的平均得分,如下表所示:
球队的男子的平均身高与本次比赛的平均得分,如下表所示:
球队 |
|
|
|
|
|
平均身高 | 170 | 174 | 176 | 181 | 179 |
平均得分 | 62 | 64 | 66 | 70 | 68 |
(1)根据表中数据,求 ![]() 关于
关于 ![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到 ![]() );
);
(2)若 ![]() 队平均身高为
队平均身高为 ![]()
![]() ,根据(1)中所求得的回归方程,预测
,根据(1)中所求得的回归方程,预测 ![]() 队的平均得分.(精确到个位) 注:回归方程
队的平均得分.(精确到个位) 注:回归方程 ![]() 中斜率和截距最小二乘估计公式分别为
中斜率和截距最小二乘估计公式分别为 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A1 , A2为椭圆 ![]() =1的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1 , A2的三点,直线QA1 , QA2 , OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=( )
=1的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1 , A2的三点,直线QA1 , QA2 , OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=( ) 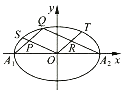
A.5
B.3+ ![]()
C.9
D.14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com