
分析 (1)an+1=3an+3n,将其转化为$\frac{{a}_{n+1}}{{3}^{n}}$-$\frac{{a}_{n}}{{3}^{n-1}}$=1,$\frac{{a}_{1}}{{3}^{0}}$=2,则数列{$\frac{{a}_{n}}{{3}^{n-1}}$}是以2为首项,1为公差的等差数列,利用等差数列通项公式即可求得an;
(2)利用“错位相减法”即可求得数列{an}的前n项和为Sn,由Sn+1>Sn知数列{Sn}为递增数列,Sn≥S1=2恒成立.
解答 解:(1)由an+1=3an+3n.
$\frac{{a}_{n+1}}{{3}^{n}}$-$\frac{{a}_{n}}{{3}^{n-1}}$=1,
$\frac{{a}_{1}}{{3}^{0}}$=2,
则数列{$\frac{{a}_{n}}{{3}^{n-1}}$}是以2为首项,1为公差的等差数列,
$\frac{{a}_{n}}{{3}^{n-1}}$=2+(n-1)=n+1,即${a_n}=(n+1){3^{n-1}}$,
数列{an}的通项公式${a_n}=(n+1){3^{n-1}}$;
(2)证明:${S_n}=2×{3^0}+3×{3^1}+4×{3^2}+…+n×{3^{n-2}}+(n+1){3^{n-1}}$①
$3{S_n}=2×{3^1}+3×{3^2}+4×{3^3}+…+n×{3^{n-1}}+(n+1){3^n}$②
①-②得$-2{S_n}=2×{3^0}+{3^1}+{3^2}+{3^3}+…+{3^{n-1}}-(n+1){3^n}$,
$-2{S_n}=2+\frac{{3-{3^n}}}{1-3}-(n+1){3^n}$,
$-2{S_n}=\frac{1}{2}-(n+\frac{1}{2}){3^n}$,
${S_n}=-\frac{1}{4}+(\frac{2n+1}{4}){3^n}$,
由Sn+1>Sn知数列{Sn}为递增数列,
∴Sn≥S1=2
综上所述原命题成立.
点评 本题考查利用递推公式求等差数列通项公式,利用“错位相减法”求数列的前n项和为Sn,考查综合分析问题及解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
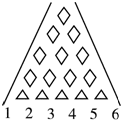 某个游戏中,一个珠子按如图所示的通道,由上至下的滑下,从最下面的六个出口出来,规定猜中者为胜,如果某人在该游戏中,猜得珠子从3号口出来,那么他取胜的概率为$\frac{5}{16}$.
某个游戏中,一个珠子按如图所示的通道,由上至下的滑下,从最下面的六个出口出来,规定猜中者为胜,如果某人在该游戏中,猜得珠子从3号口出来,那么他取胜的概率为$\frac{5}{16}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3,5} | B. | {1,2,4,5} | C. | {1,5} | D. | {2,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 线段 | B. | 直线 | C. | 圆 | D. | 射线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com