
【题目】某手机生产厂商为迎接5G时代的到来,要生产一款5G手机,在生产之前,该公司对手机屏幕的需求尺寸进行社会调查,共调查了400人,将这400人按对手机屏幕的需求尺寸分为6组,分别是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:英寸),得到如下频率分布直方图:
(单位:英寸),得到如下频率分布直方图:

其中,屏幕需求尺寸在![]() 的一组人数为50人.
的一组人数为50人.
(1)求a和b的值;
(2)用分层抽样的方法在屏幕需求尺寸为![]() 和
和![]() 两组人中抽取6人参加座谈,并在6人中选择2人做代表发言,则这2人来自同一分组的概率是多少?
两组人中抽取6人参加座谈,并在6人中选择2人做代表发言,则这2人来自同一分组的概率是多少?
(3)若以厂家此次调查结果的频率作为概率,市场随机调查两人,这两人屏幕需求尺寸分别在![]() 和
和![]() 的概率是多少?
的概率是多少?
【答案】(1)![]() ,
,![]() .(2)
.(2)![]() (3)0.035.
(3)0.035.
【解析】
(1)根据屏幕需求尺寸在![]() 的一组频数为50求解区间对应的频率进而求
的一组频数为50求解区间对应的频率进而求![]() ,再根据频率分布直方图的面积之和为1求解
,再根据频率分布直方图的面积之和为1求解![]() 即可.
即可.
(2)利用分层抽样的方法以及古典概型的方法求解即可.
(3)利用独立事件的概率公式求解即可.
解:(1)由已知,屏幕需求尺寸在![]() 的一组频数为50,
的一组频数为50,
所以其频率为![]() ,
,
又因为组距为0.5,所以![]() ,
,
又因为![]() ,
,
解得![]() ,所以
,所以![]() ,
,![]() .
.
(2)由直方图知,两组人数分别为![]() ,
,![]() ,
,
若分层抽取6人,则在![]() 组中抽取2人,设为
组中抽取2人,设为![]() ,
,![]() ;在
;在![]() 组中抽取4分,设为
组中抽取4分,设为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
样本空间![]() 共15个基本事件,
共15个基本事件,
记两人来自同一组为事件![]() ,
,![]() 共7个基本事件.
共7个基本事件.
所以![]() .
.
(3)记事件![]() 为屏幕需求尺寸在
为屏幕需求尺寸在![]() ,事件
,事件![]() 为屏幕需求尺寸在
为屏幕需求尺寸在![]() ,若以调查频率作为概率,则
,若以调查频率作为概率,则![]() ,
,![]() ,
,![]() ,
,
所以两人分别需求屏幕尺寸在![]() 和
和![]() 的概率为0.035.
的概率为0.035.


科目:高中数学 来源: 题型:
【题目】已知有限集![]() . 如果
. 如果![]() 中元素
中元素![]() 满足
满足![]() ,就称
,就称![]() 为“复活集”,给出下列结论:
为“复活集”,给出下列结论:
①集合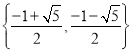 是“复活集”;
是“复活集”;
②若![]() ,且
,且![]() 是“复活集”,则
是“复活集”,则![]() ;
;
③若![]() ,则
,则![]() 不可能是“复活集”;
不可能是“复活集”;
④若![]() ,则“复活集”
,则“复活集”![]() 有且只有一个,且
有且只有一个,且![]() .
.
其中正确的结论是____________.(填上你认为所有正确的结论序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 和直线
和直线![]() 在该直角坐标系下的普通方程;
在该直角坐标系下的普通方程;
(2)动点![]() 在曲线
在曲线![]() 上,动点
上,动点![]() 在直线
在直线![]() 上,定点
上,定点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com