
【题目】已知函数![]()
![]() .
.
(1)若![]() 是
是![]() 的极值点,求a的值及
的极值点,求a的值及![]() 的单调区间;
的单调区间;
(2)若对任意![]() ,不等式
,不等式![]() 成立,求a的取值范围.
成立,求a的取值范围.
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() ,
,![]() 是
是![]() 轴上关于原点
轴上关于原点![]() 对称的两定点,点
对称的两定点,点![]() 满足
满足![]() ,点
,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的方程;
的方程;
(2)过![]() 的直线与
的直线与![]() 交于点
交于点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,
,![]() 的中垂线分别与
的中垂线分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,问
,问![]() 是否成立?若成立,求出直线
是否成立?若成立,求出直线![]() 的方程;若不成立,请说明理由.
的方程;若不成立,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,数列
,数列![]() 中的每一项均在集合
中的每一项均在集合![]() 中,且任意两项不相等,又对于任意的整数
中,且任意两项不相等,又对于任意的整数![]() ,均有
,均有![]() .例如
.例如![]() 时,数列
时,数列![]() 为
为![]() 或
或![]() .
.
(1)当![]() 时,试求满足条件的数列
时,试求满足条件的数列![]() 的个数;
的个数;
(2)当![]() ,求所有满足条件的数列
,求所有满足条件的数列![]() 的个数.
的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知点
中,已知点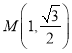 ,
,![]() 的参数方程为
的参数方程为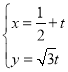 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让居民了解垃圾分类,养成垃圾分类的习惯,让绿色环保理念深入人心.某市将垃圾分为四类:可回收物,餐厨垃圾,有害垃圾和其他垃圾.某班按此四类由10位同学组成四个宣传小组,其中可回收物与餐厨垃圾宣传小组各有2位同学,有害垃圾与其他垃圾宣传小组各有3位同学.现从这10位同学中选派5人到某小区进行宣传活动,则每个宣传小组至少选派1人的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊数学家阿波罗尼奥斯发现:平面上到两定点![]() ,
,![]() 距离之比为常数
距离之比为常数![]() 且
且![]() 的点的轨迹是一个圆心在直线
的点的轨迹是一个圆心在直线![]() 上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体
上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体![]() 中,
中,![]() ,点
,点![]() 在棱
在棱![]() 上,
上,![]() ,动点
,动点![]() 满足
满足![]() .若点
.若点![]() 在平面
在平面![]() 内运动,则点
内运动,则点![]() 所形成的阿氏圆的半径为________;若点
所形成的阿氏圆的半径为________;若点![]() 在长方体
在长方体![]() 内部运动,
内部运动,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为
为![]() 的中点,则三棱锥
的中点,则三棱锥![]() 的体积的最小值为___________.
的体积的最小值为___________.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天津市某学校组织教师进行“学习强国”知识竞赛,规则为:每位参赛教师都要回答3个问题,且对这三个问题回答正确与否相互之间互不影响,若每答对1个问题,得1分;答错,得0分,最后按照得分多少排出名次,并分一、二、三等奖分别给予奖励.已知对给出的3个问题,教师甲答对的概率分别为![]() ,
,![]() ,p.若教师甲恰好答对3个问题的概率是
,p.若教师甲恰好答对3个问题的概率是![]() ,则
,则![]() ________;在前述条件下,设随机变量X表示教师甲答对题目的个数,则X的数学期望为________.
________;在前述条件下,设随机变量X表示教师甲答对题目的个数,则X的数学期望为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,若a=5![]() sin(B
sin(B![]() ),c=5且O为△ABC的外心,G为△ABC的重心,则OG的最小值为( )
),c=5且O为△ABC的外心,G为△ABC的重心,则OG的最小值为( )
A.![]() 1B.
1B.![]() C.
C.![]() 1D.
1D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com