练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本题满分12分）已知函数.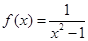

    （1）设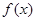的定义域为A，求集合A；

    （2）判断函数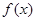在（1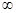，+）上单调性，并用定义加以证明.

     

    【答案】

    （1）；（2）用定义证明函数单调性的步骤；一设二作差三变形四判断符号五得出结论。

    【解析】

    试题分析：（1）由，得，

    所以，函数的定义域为……………………… 4分

    （2）函数在上单调递减.  ………………………………6分

    证明：任取，设，

    则

    …………………… 8分

    又，所以 故

    因此，函数在上单调递减.  ………………………12分

    考点：函数定义域的求法；用定义证明函数的单调性。

    点评：用定义证明函数单调性的步骤；一设二作差三变形四判断符号五得出结论。尤其是其中的三变形的步骤特别重要，最好变成几个因式乘积的形式。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （ 本题满分12分 ）
    已知函数f（x）=cos4x-2sinxcosx-sin4x
    （I）求f（x）的最小正周期；
    （II）若x∈[0，
    π2
    ]    ，求f（x）的最大值，最小值．

    查看答案和解析>>

    科目：高中数学 来源：安徽省合肥一中、六中、一六八中学2010-2011学年高二下学期期末联考数学（理 题型：解答题

    （本题满分12分）已知△的三个内角、、所对的边分别为、、.，且.（1）求的大小；（2）若.求.

    查看答案和解析>>

    科目：高中数学 来源：2011届本溪县高二暑期补课阶段考试数学卷 题型：解答题

    （本题满分12分）已知各项均为正数的数列，
    的等比中项。
    （1）求证：数列是等差数列；（2）若的前n项和为Tn,求Tn。

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年广东省揭阳市高三调研检测数学理卷 题型：解答题

    （本题满分12分）

    已知椭圆：的长轴长是短轴长的倍，，是它的左，右焦点．

    （1）若，且，，求、的坐标；

    （2）在（1）的条件下，过动点作以为圆心、以1为半径的圆的切线（是切点），且使，求动点的轨迹方程．

     

    查看答案和解析>>

    科目：高中数学 来源：2010年辽宁省高二上学期10月月考理科数学卷 题型：解答题

    （本题满分12分）已知椭圆的长轴，短轴端点分别是A,B，从椭圆上一点M向x轴作垂线，恰好通过椭圆的左焦点，向量与是共线向量

    （1）求椭圆的离心率

    （2）设Q是椭圆上任意一点，分别是左右焦点，求的取值范围

     

    查看答案和解析>>

    同步练习册答案