
ЁОЬтФПЁПвбжЊAЃЈx0 ЃЌ 0ЃЉЃЌBЃЈ0ЃЌy0ЃЉСНЕуЗжБ№дкxжсКЭyжсЩЯдЫЖЏЃЌЧв|AB|=1ЃЌШєЖЏЕуPЃЈxЃЌyЃЉТњзу ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓГіЖЏЕуPЕФЙьМЃЖдгІЧњЯпCЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉвЛЬѕзнНиОрЮЊ2ЕФжБЯпl1гыЧњЯпCНЛгкPЃЌQСНЕуЃЌШєвдPQжБОЖЕФдВЧЁЙ§дЕуЃЌЧѓГіжБЯпЗНГЬЃЛ
ЃЈ3ЃЉжБЯпl2ЃКx=ty+1гыЧњЯпCНЛгкAЁЂBСНЕуЃЌEЃЈ1ЃЌ0ЃЉЃЌЪдЮЪЃКЕБtБфЛЏЪБЃЌЪЧЗёДцдквЛжБЯпl2 ЃЌ ЪЙЁїABEЕФУцЛ§ЮЊ ![]() ЃПШєДцдкЃЌЧѓГіжБЯпl2ЕФЗНГЬЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЃПШєДцдкЃЌЧѓГіжБЯпl2ЕФЗНГЬЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКвђЮЊ ![]() ЃЌ
ЃЌ
МД ![]() ЃЌ
ЃЌ
Ыљвд ![]() ЃЌ
ЃЌ
Ыљвд ![]()
гжвђЮЊ|AB|=1ЃЌЫљвд ![]() ЃЌ
ЃЌ
МДЃК ![]() ЃЌ
ЃЌ
МД ![]() ЃЌ
ЃЌ
ЫљвдЭждВЕФБъзМЗНГЬЮЊ ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉНтЃКжБЯпl1аБТЪБиДцдкЃЌЧвзнНиОрЮЊ2ЃЌЩшжБЯпЮЊy=kx+2СЊСЂжБЯпl1КЭЭждВЗНГЬ 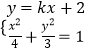 ЃЌ
ЃЌ
ЕУЃКЃЈ3+4k2ЃЉx2+16kx+4=0ЃЌ
гЩЁїЃО0ЃЌЕУ ![]() ЃЈ*ЃЉЃЌ
ЃЈ*ЃЉЃЌ
ЩшPЃЈx1ЃЌy1ЃЉЃЌQЃЈx2ЃЌy2ЃЉЃЌ
дђ ![]() ЃЈ1ЃЉ
ЃЈ1ЃЉ
вдPQжБОЖЕФдВЧЁЙ§дЕуЃЌ
ЫљвдOPЁЭOQЃЌ ![]() ЃЌ
ЃЌ
МДx1x2+y1y2=0ЃЌ
вВМДx1x2+ЃЈkx1+2ЃЉЃЈkx2+2ЃЉ=0ЃЌ
МДЃЈ1+k2ЃЉx1x2+2kЃЈx1+x2ЃЉ+4=0ЃЌ
НЋЃЈ1ЃЉЪНДњШыЃЌЕУ ![]() Љ
Љ ![]() +4=0ЃЌ
+4=0ЃЌ
МД4ЃЈ1+k2ЃЉЉ32k2+4ЃЈ3+4k2ЃЉ=0ЃЌ
НтЕУ ![]() ЃЌТњзуЃЈ*ЃЉЪНЃЌ
ЃЌТњзуЃЈ*ЃЉЪНЃЌ
Ыљвд ![]() ЃЎ
ЃЎ
ЫљвджБЯпЗНГЬЮЊy=ЁР ![]() x+2
x+2
ЃЈ3ЃЉНтЃКгЩЗНГЬзщ 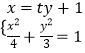 ЃЌЕУЃЈ3t2+4ЃЉy2+6tyЉ9=0ЃЈ*ЃЉ
ЃЌЕУЃЈ3t2+4ЃЉy2+6tyЉ9=0ЃЈ*ЃЉ
ЩшAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЌ
дђ ![]()
Ыљвд ![]() ЃЌ
ЃЌ
вђЮЊжБЯпlЃКx=ty+1Й§ЕуFЃЈ1ЃЌ0ЃЉЃЌ
ЫљвдSЁїABE= ![]() |EF||y1Љy2|=
|EF||y1Љy2|= ![]() ЁС2ЁС
ЁС2ЁС ![]() =
= ![]()
Сю= ![]() =2
=2 ![]() ЃЌдђ
ЃЌдђ ![]() ВЛГЩСЂ
ВЛГЩСЂ
ЙЪВЛДцдкжБЯпlТњзуЬтвт
ЁОНтЮіЁПЃЈ1ЃЉИљОнЯђСПЕФзјБъдЫЫуЃЌвдМА|AB|=1ЃЌЕУЕНЭждВЕФБъзМЗНГЬЮЊ ![]() ЃЎЃЈ2ЃЉжБЯпl1аБТЪБиДцдкЃЌЧвзнНиОрЮЊ2ЃЌИљОнжБЯпгыЭждВЕФЮЛжУЙиЯЕЃЌМДПЩЧѓГіkЕФжЕЃЌЮЪЬтЕУвдНтОіЃЎЃЈ3ЃЉИљОнжБЯпКЭЭждВЖюЮЛжУЙиЯЕЃЌвдМАШ§НЧаЮЕФУцЛ§ЙЋЪНЕУЕНSЁїABE=
ЃЎЃЈ2ЃЉжБЯпl1аБТЪБиДцдкЃЌЧвзнНиОрЮЊ2ЃЌИљОнжБЯпгыЭждВЕФЮЛжУЙиЯЕЃЌМДПЩЧѓГіkЕФжЕЃЌЮЪЬтЕУвдНтОіЃЎЃЈ3ЃЉИљОнжБЯпКЭЭждВЖюЮЛжУЙиЯЕЃЌвдМАШ§НЧаЮЕФУцЛ§ЙЋЪНЕУЕНSЁїABE= ![]() ЃЌСю=
ЃЌСю= ![]() =2
=2 ![]() ЃЌдђ
ЃЌдђ ![]() ВЛГЩСЂЃЌЮЪЬтЕУвдНтОіЃЎ
ВЛГЩСЂЃЌЮЪЬтЕУвдНтОіЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉШєКЏЪ§![]() дкЦфЖЈвхгђЩЯЮЊЕЅЕїдіКЏЪ§ЃЌЧѓ
дкЦфЖЈвхгђЩЯЮЊЕЅЕїдіКЏЪ§ЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉМЧ![]() ЕФЕМКЏЪ§ЮЊ
ЕФЕМКЏЪ§ЮЊ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌжЄУїЃК
ЪБЃЌжЄУїЃК![]() ДцдкМЋаЁжЕЕу
ДцдкМЋаЁжЕЕу![]() ЃЌЧв
ЃЌЧв![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшЯђСП![]() ЃЌ
ЃЌ![]() ЃЌСюКЏЪ§
ЃЌСюКЏЪ§![]() ЃЌШєКЏЪ§
ЃЌШєКЏЪ§![]() ЕФВПЗжЭМЯѓШчЭМЫљЪОЃЌЧвЕу
ЕФВПЗжЭМЯѓШчЭМЫљЪОЃЌЧвЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() .
.

ЃЈ1ЃЉЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉЧѓКЏЪ§![]() ЕФЕЅЕїдіЧјМфМАЖдГЦжсЗНГЬЃЛ
ЕФЕЅЕїдіЧјМфМАЖдГЦжсЗНГЬЃЛ
ЃЈ3ЃЉШєАбЗНГЬ![]() ЕФе§ЪЕИљДгаЁЕНДѓвРДЮХХСаЮЊ
ЕФе§ЪЕИљДгаЁЕНДѓвРДЮХХСаЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЯиНЬг§ОжЮЊСЫМьВщБОЯиМзЁЂввСНЫљбЇаЃЕФбЇЩњЖдАВШЋжЊЪЖЕФбЇЯАЧщПіЃЌдкетСНЫљбЇаЃНјааСЫАВШЋжЊЪЖВтЪдЃЌЫцЛњдкетСНЫљбЇаЃИїГщШЁ20УћбЇЩњЕФПМЪдГЩМЈзїЮЊбљБОЃЌГЩМЈДѓгкЛђЕШгк80ЗжЕФЮЊгХауЃЌЗёдђЮЊВЛгХауЃЌЭГМЦНсЙћШчЯТЭМЃК


МзаЃ вваЃ
ЃЈ1ЃЉДгвваЃГЩМЈгХауЕФбЇЩњжаШЮбЁСНУћЃЌЧѓетСНУћбЇЩњЕФГЩМЈЧЁгавЛИіТфдк![]() ФкЕФИХТЪЃЛ
ФкЕФИХТЪЃЛ
ЃЈ2ЃЉгЩвдЩЯЪ§ОнЭъГЩЯТУцСаСЊБэЃЌВЂЛиД№ФмЗёдкЗИДэЕФИХТЪВЛГЌЙ§0.1ЕФЧАЬсЯТШЯЮЊбЇЩњЕФГЩМЈгыСНЫљбЇаЃЕФбЁдёгаЙиЁЃ
МзаЃ | вваЃ | змМЦ | |
гХау | |||
ВЛгХау | |||
змМЦ |
![]()
ВЮПМЪ§Он | PЃЈK2Ёнk0ЃЉ | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | span>3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшЪ§Са{an}ЕФЧАnЯюКЭЮЊ ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЪ§Са{an}ЕФЭЈЯюЙЋЪНanЃЛ
ЃЈ2ЃЉЪЧЗёДцдке§ећЪ§nЃЌЪЙЕУ ![]() ЃПШєДцдкЃЌЧѓГіnжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЃПШєДцдкЃЌЧѓГіnжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋКЏЪ§fЃЈxЃЉ=sinЃЈ2x+ІеЃЉ+ ![]() cosЃЈ2x+ІеЃЉЃЈ0ЃМІеЃМІаЃЉЭМЯѓЯђзѓЦНвЦ
cosЃЈ2x+ІеЃЉЃЈ0ЃМІеЃМІаЃЉЭМЯѓЯђзѓЦНвЦ ![]() ИіЕЅЮЛКѓЃЌЕУЕНКЏЪ§ЕФЭМЯѓЙигкЕуЃЈ
ИіЕЅЮЛКѓЃЌЕУЕНКЏЪ§ЕФЭМЯѓЙигкЕуЃЈ ![]() ЃЌ0ЃЉЖдГЦЃЌдђКЏЪ§gЃЈxЃЉ=cosЃЈx+ІеЃЉдк[Љ
ЃЌ0ЃЉЖдГЦЃЌдђКЏЪ§gЃЈxЃЉ=cosЃЈx+ІеЃЉдк[Љ ![]() ЃЌ
ЃЌ ![]() ]ЩЯЕФзюаЁжЕЪЧЃЈ ЃЉ
]ЩЯЕФзюаЁжЕЪЧЃЈ ЃЉ
A.Љ ![]()
B.Љ ![]()
C.![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЧњЯп
жаЃЌЧњЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌдквддЕуЮЊМЋЕуЃЌ
ЮЊВЮЪ§ЃЉЃЌдквддЕуЮЊМЋЕуЃЌ ![]() жсе§АыжсЮЊМЋжсЕФМЋзјБъЯЕжаЃЌжБЯп
жсе§АыжсЮЊМЋжсЕФМЋзјБъЯЕжаЃЌжБЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФЦеЭЈЗНГЬКЭжБЯп
ЕФЦеЭЈЗНГЬКЭжБЯп![]() ЕФЧуаБНЧЃЛ
ЕФЧуаБНЧЃЛ
ЃЈ2ЃЉЩшЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() КЭЧњЯп
КЭЧњЯп![]() НЛгк
НЛгк![]() СНЕуЃЌЧѓ
СНЕуЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪЕЪ§aЁЂbТњзуЃКaЃО0ЃЌbЃО0ЃЎ
ЃЈ1ЃЉШєxЁЪRЃЌЧѓжЄЃК|x+a|+|xЉb|Ён2 ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉШєa+b=1ЃЌЧѓжЄЃК ![]() +
+ ![]() +
+ ![]() Ён12ЃЎ
Ён12ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊдВ![]() ЃК
ЃК ![]() ЃЌЕу
ЃЌЕу![]() .
.
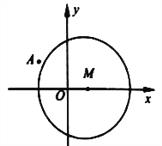
ЃЈ1ЃЉЧѓОЙ§Еу![]() ЧвгыдВ
ЧвгыдВ![]() ЯрЧаЕФжБЯп
ЯрЧаЕФжБЯп![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЙ§Еу![]() ЕФжБЯпгыдВ
ЕФжБЯпгыдВ![]() ЯрНЛгк
ЯрНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌ
СНЕуЃЌ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЌЧѓЯпЖЮ
ЕФжаЕуЃЌЧѓЯпЖЮ![]() ГЄЖШЕФШЁжЕЗЖЮЇ.
ГЄЖШЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com