
(本大题13分)设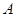 、
、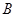 为函数
为函数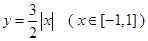 图象上不同的两个点,
图象上不同的两个点,
且 AB∥ 轴,又有定点
轴,又有定点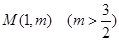 ,已知
,已知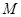 是线段
是线段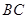 的中点.
的中点.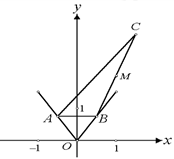
⑴ 设点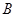 的横坐标为
的横坐标为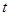 ,写出
,写出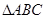 的面积
的面积 关于
关于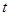 的函数
的函数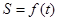 的表达式;
的表达式;
⑵ 求函数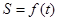 的最大值,并求此时点
的最大值,并求此时点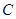 的坐标。
的坐标。
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:解答题
某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖4节车厢,一日能来回16次, 如果每次拖7节车厢,则每日能来回10次.
(1)若每日来回的次数是车头每次拖挂车厢节数的一次函数,求此一次函数解析式:
(2)在(1)的条件下,每节车厢能载乘客110人.问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=x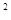 +2ax+2, x
+2ax+2, x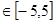 .
.
(1)当a=-1时,求函数的最大值和最小值;
(2) 若y=f(x)在区间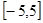 上是单调 函数,求实数 a的取值范围.
上是单调 函数,求实数 a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某服装厂生产一种服装,每件服装的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出场单价就降低0.02元,根据市场调查,销售商一次订购量不会超过600件.
(1)设一次订购x件,服装的实际出厂单价为p元,写出函数p=f(x)的表达式;
(2)当销售商一次订购多少件服装时,该厂获得的利润最大?其最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某沿海地区养殖的一种特色海鲜上市时间仅能持续5个月,预测上市初期和后期会因供应不足使价格呈持续上涨态势,而中期又将出现供大于求使价格连续下跌.现有三种价格模拟函数:①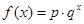 ;②
;②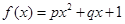 ;③
;③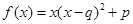 .(以上三式中、
.(以上三式中、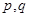 均为常数,且
均为常数,且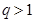 )
)
(I)为准确研究其价格走势,应选哪种价格模拟函数(不必说明理由)
(II)若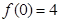 ,
,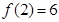 ,求出所选函数
,求出所选函数 的解析式(注:函数定义域是
的解析式(注:函数定义域是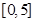 .其中
.其中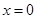 表示8月1日,
表示8月1日,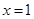 表示9月1日,…,以此类推);
表示9月1日,…,以此类推);
(III)在(II)的条件下研究下面课题:为保证养殖户的经济效益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该海鲜将在哪几个月份内价格下跌.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了保护水资源,提倡节约用水,某市对居民生活用水收费标准如下:每户每月用水不超过6吨时每吨3元,当用水超过6吨但不超过15吨时,超过部分每吨5元,当用水超过15吨时,超过部分每吨10元。
(1)求水费y(元)关于用水量x(吨)之间的函数关系式;
(2)若某户居民某月所交水费为93元,试求此用户该月的用水量。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
函数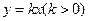 的图象与函数
的图象与函数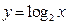 的图象交于两点
的图象交于两点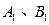 (
(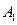 在线段
在线段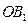 上,
上,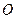 为坐标原点),过
为坐标原点),过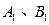 作
作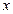 轴的垂线,垂足分别为
轴的垂线,垂足分别为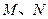 ,并且
,并且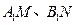 分别交函数
分别交函数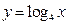 的图象于
的图象于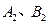 两点.
两点.
(1)试探究线段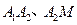 的大小关系;
的大小关系;
(2)若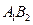 平行于
平行于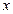 轴,求四边形
轴,求四边形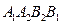 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是P和Q(万元),它们与投入资金x(万元)的关系有经验公式:P=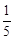 x,Q=
x,Q=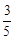
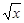 .今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少,能获得的最大利润为多少?
.今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少,能获得的最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com