
分析 (Ⅰ)根据函数奇偶性的定义求出a的值即可,
(Ⅱ)根据条件判断函数的单调性,利用函数奇偶性和单调性的性质进行转化求解即可.
解答 解:(Ⅰ)因为函数$f(x)=a-\frac{2}{{{2^x}+1}}$是R上的奇函数,所以f(0)=0.(2分)
即$a-\frac{2}{{{2^0}+1}}=0$,解得a=1.(3分)
(Ⅱ)由(Ⅰ),得$f(x)=1-\frac{2}{{{2^x}+1}}$.
因为f(x)是R上的奇函数,由f(1-m)+f(1-m2)<0,
得f(1-m)<-f(1-m2),即f(1-m)<f(m2-1).(5分)
下面证明f(x)在R是增函数.
设x1,x2∈R且x1<x2,则$f({x_1})-f({x_2})=({1-\frac{2}{{{2^{x_1}}+1}}})-({1-\frac{2}{{{2^{x_2}}+1}}})=\frac{{2({{2^{x_1}}-{2^{x_2}}})}}{{({{2^{x_1}}+1})({{2^{x_2}}+1})}}$(6分)
因为x1<x2,所以${2^{x_1}}<{2^{x_2}}$,${2^{x_1}}-{2^{x_2}}<0$,而${2^{x_1}}+1>0,{2^{x_2}}+1>0$,
所以$\frac{{2({{2^{x_1}}-{2^{x_2}}})}}{{({{2^{x_1}}+1})({{2^{x_2}}+1})}}<0$,
即f(x1)<f(x2),所以$f(x)=a-\frac{2}{{{2^x}+1}}$是R上的增函数.(8分)
当x∈(-1,1)时,由f(1-m)<f(m2-1)得$\left\{\begin{array}{l}-1<1-m<1\\-1<{m^2}-1<1\\ 1-m<{m^2}-1\end{array}\right.$,(10分)
解得$1<m<\sqrt{2}$.
所以,当x∈(-1,1)时,满足不等式f(1-m)+f(1-m2)<0的实数m的取值范围是$(1,\sqrt{2})$.(12分)
点评 本题主要考查不等式的求解,利用函数奇偶性的性质求出函数的解析式以及利用函数单调性和奇偶性将不等式进行转化是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
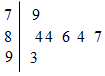 如图是2013年中央电视台举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图是2013年中央电视台举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 85,1.6 | B. | 84,4 | C. | 84,1.6 | D. | 85,4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 140 | B. | 110 | C. | 70 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
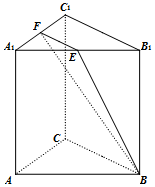 三棱柱ABC-A1B1C1中,AB=AC,侧棱AA1⊥平面ABC,E,F分别为A1B1,A1C1的中点.
三棱柱ABC-A1B1C1中,AB=AC,侧棱AA1⊥平面ABC,E,F分别为A1B1,A1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com