
【题目】已知函数f(x)=x2+ax+blnx(a,b∈R),曲线y=f(x)在点(1,f(1))处的切线方程为2x﹣y﹣2=0.
(1)判断f(x)在定义域内的单调性,并说明理由;
(2)若对任意的x∈(1,+∞),不等式f(x)≤m(ex﹣1﹣1)恒成立,求实数m的取值范围.
【答案】(1)f(x)在(0,+∞)上为增函数;见解析(2)[2,+∞)
【解析】
求出原函数的导函数,利用f′(1)=2及f(1)=0联立不等式组求解a,b的值,则函数解析式可求.(1)由f′(x)>0在(0,+∞)上恒成立,可得f(x)在(0,+∞)上为增函数;
(2)对任意的x∈(1,+∞),不等式f(x)≤m(ex﹣1﹣1)恒成立,即x2﹣x+lnx≤m(ex﹣1﹣1)恒成立,令g(x)=m(ex﹣1﹣1)﹣x2+x﹣lnx,求其导函数,分析可知当m≥2时,g′(x)>g′(1)≥0,g(x)单调递增,则g(x)>g(1)=0;当0<m<2时,g′(x)=0在(1,+∞)上必有实数根,设最小的正数根为x0,当x∈(1,x0)时,g′(x)<0,g(x)单调递减,则g(x)<g(1)=0,与题设不符;当m≤0时,g′(x)<0,则g(x)单调递减,g(x)<g(1)=0,与题意不符.
解:由f(x)=x2+ax+blnx,得f′(x)=2x+a![]() (x>0).
(x>0).
由曲线y=f(x)在点(1,f(1))处的切线方程为2x﹣y﹣2=0,
得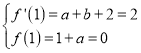 ,即a=﹣1,b=1.
,即a=﹣1,b=1.
∴f(x)=x2﹣x+lnx.
(1)∵f′(x)=2x﹣1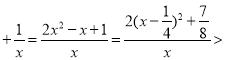 0在(0,+∞)上恒成立,
0在(0,+∞)上恒成立,
∴f(x)在(0,+∞)上为增函数;
(2)由(1)得,f(x)=x2﹣x+lnx,
对任意的x∈(1,+∞),不等式f(x)≤m(ex﹣1﹣1)恒成立,
即x2﹣x+lnx≤m(ex﹣1﹣1)恒成立,
令g(x)=m(ex﹣1﹣1)﹣f(x)=m(ex﹣1﹣1)﹣x2+x﹣lnx,
则g′(x)![]() ,注意到g(1)=0,g′(1)=m﹣2,
,注意到g(1)=0,g′(1)=m﹣2,
要使得对任意的x∈(1,+∞),不等式f(x)≤m(ex﹣1﹣1)恒成立,即g(x)≥0,
则必有g′(x)在(1,1+δ)(其中δ为任意小的正数)大于0,亦有g′(1)≥0,则m≥2.
当m≥2时,令u(x)=g′(x)![]() ,
,
u′(x)![]() 2ex﹣1﹣2>0.
2ex﹣1﹣2>0.
∴u(x)在(1,+∞)上单调递增,则g′(x)>g′(1)≥0,
∴g(x)单调递增,则g(x)>g(1)=0;
当0<m<2时,g′(1)=m﹣2<0,当x→+∞时,g′(x)→+∞,
则g′(x)=0在(1,+∞)上必有实数根,设最小的正数根为x0,
则当x∈(1,x0)时,g′(x)<0,g(x)单调递减,则g(x)<g(1)=0,与题设不符;
当m≤0时,g′(x)![]() 0,则g(x)单调递减,g(x)<g(1)=0,与题意不符.
0,则g(x)单调递减,g(x)<g(1)=0,与题意不符.
综上所述,m的取值范围为[2,+∞).


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线E的极坐标方程为![]() ,直线l的参数方程为
,直线l的参数方程为![]() (t为参数).点P为曲线E上的动点,点Q为线段OP的中点.
(t为参数).点P为曲线E上的动点,点Q为线段OP的中点.
(1)求点Q的轨迹(曲线C)的直角坐标方程;
(2)若直线l交曲线C于A,B两点,点![]() 恰好为线段AB的三等分点,求直线l的普通方程.
恰好为线段AB的三等分点,求直线l的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱锥![]() 中,
中,![]() 是边长为3的等边三角形,点M是
是边长为3的等边三角形,点M是![]() 的重心,过点M作与平面PAC垂直的平面
的重心,过点M作与平面PAC垂直的平面![]() ,平面
,平面![]() 与截面PAC交线段的长度为2,则平面
与截面PAC交线段的长度为2,则平面![]() 与正四棱椎
与正四棱椎![]() 表面交线所围成的封闭图形的面积可能为______________.(请将可能的结果序号填到横线上)①2;②
表面交线所围成的封闭图形的面积可能为______________.(请将可能的结果序号填到横线上)①2;②![]() ;③3; ④
;③3; ④![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图所示的三棱锥D﹣ABC的四个顶点均在球O的球面上,△ABC和△DBC所在平面相互垂直,AB=3,AC=![]() ,BC=CD=BD=2
,BC=CD=BD=2![]() ,则球O的表面积为( )
,则球O的表面积为( )
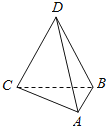
A.4π B.12π C.16π D.36π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=2sinx(sinx![]() cosx)﹣1图象向右平移
cosx)﹣1图象向右平移![]() 个单位得函数g(x)的图象,则下列命题中正确的是( )
个单位得函数g(x)的图象,则下列命题中正确的是( )
A.f(x)在(![]() ,
,![]() )上单调递增
)上单调递增
B.函数f(x)的图象关于直线x![]() 对称
对称
C.g(x)=2cos2x
D.函数g(x)的图象关于点(![]() ,0)对称
,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】很多关于整数规律的猜想都通俗易懂,吸引了大量的数学家和数学爱好者,有些猜想已经被数学家证明,如“费马大定理”,但大多猜想还未被证明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的内容是:对于每一个正整数,如果它是奇数,则将它乘以![]() 再加1;如果它是偶数,则将它除以
再加1;如果它是偶数,则将它除以![]() ;如此循环,最终都能够得到
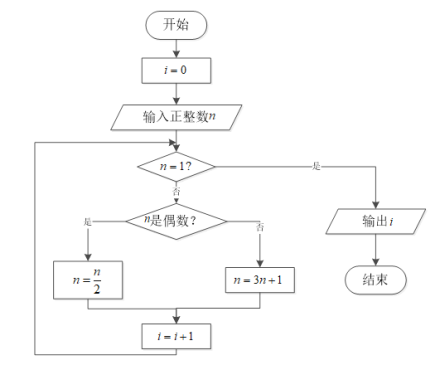
;如此循环,最终都能够得到![]() .下图为研究“角谷猜想”的一个程序框图.若输入
.下图为研究“角谷猜想”的一个程序框图.若输入![]() 的值为
的值为![]() ,则输出i的值为( )
,则输出i的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
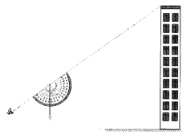
【题目】数学兴趣小组为了测量校园外一座“不可到达”建筑物的高度,采用“两次测角法”,并自制了测量工具:将一个量角器放在复印机上放大4倍复印,在中心处绑上一个铅锤,用于测量楼顶仰角(如图);推动自行车来测距(轮子滚动一周为1.753米).该小组在操场上选定A点,此时测量视线和铅锤线之间的夹角在量角器上度数为37°;推动自行车直线后退,轮子滚动了10卷达到B点,此时测量视线和铅锤线之间的夹角在量角器上度数为53°.测量者站立时的“眼高”为1.55m,根据以上数据可计算得该建筑物的高度约为___________米.(精确到0.1)
参考数据:![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com