
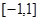 中任取两个数
中任取两个数 ,则事件“
,则事件“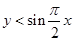 ”发生的概率为 .
”发生的概率为 .科目:高中数学 来源:不详 题型:单选题
| A.8.68 | B.16.32 | C.17.32 | D.7.68 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
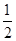 和
和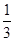 , 求:
, 求:查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
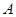 区域返券60元;停在
区域返券60元;停在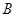 区域返券30元;停在
区域返券30元;停在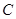 区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.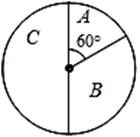
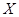 (元),求随机变量
(元),求随机变量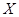 的分布列和数学期望.
的分布列和数学期望. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
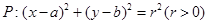 被y轴所截的弦长为2,被x轴分成两段弧,且弧长之比等于
被y轴所截的弦长为2,被x轴分成两段弧,且弧长之比等于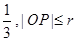 (其中
(其中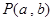 为圆心,O为坐标原点)。
为圆心,O为坐标原点)。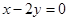 上的投影为A,求事件“在圆P内随机地投入一点,使这一点恰好在
上的投影为A,求事件“在圆P内随机地投入一点,使这一点恰好在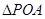 内”的概率的最大值
内”的概率的最大值查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com