
【题目】直角坐标系xOy中,已知MN是圆C:(x﹣2)2+(y﹣3)2=2的一条弦,且CM⊥CN,P是MN的中点.当弦MN在圆C上运动时,直线l:x﹣y﹣5=0上总存在两点A,B,使得![]() 恒成立,则线段AB长度的最小值是_____.
恒成立,则线段AB长度的最小值是_____.
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xcos+a,a∈R.
(I)求曲线y=f(x)在点x=![]() 处的切线的斜率;
处的切线的斜率;
(II)判断方程f '(x)=0(f '(x)为f(x)的导数)在区间(0,1)内的根的个数,说明理由;
(III)若函数F(x)=xsinx+cosx+ax在区间(0,1)内有且只有一个极值点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,新冠肺炎疫情袭击全国,对人民生命安全和生产生活造成严重影响.在党和政府强有力的抗疫领导下,我国控制住疫情后,一方面防止境外疫情输入,另一方面逐步复工复产,减轻经济下降对企业和民众带来的损失.为降低疫情影响,某厂家拟在2020年举行某产品的促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() 万件与年促销费用
万件与年促销费用![]() 万元(
万元(![]() )满足
)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是2万件.已知生产该产品的固定投入为8万元,每生产一万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(此处每件产品年平均成本按
为常数),如果不搞促销活动,则该产品的年销售量只能是2万件.已知生产该产品的固定投入为8万元,每生产一万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(此处每件产品年平均成本按![]() 元来计算)
元来计算)
(1)将2020年该产品的利润![]() 万元表示为年促销费用
万元表示为年促销费用![]() 万元的函数;
万元的函数;
(2)该厂家2020年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88,若样本B数据恰好是样本A数据都加上2后所得数据,则A,B两样本的下列数字特征对应相同的是( )
A. 众数 B. 平均数
C. 中位数 D. 标准差
查看答案和解析>>
科目:高中数学 来源: 题型:
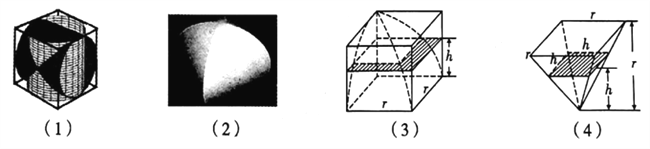
【题目】中国古代数学家刘徽在《九章算术注》中,称一个正方体内两个互相垂直的内切圆柱所围成的立体为“牟合方盖”,如图(1)(2),刘徽未能求得牟合方盖的体积,直言“欲陋形措意,惧失正理”,不得不说“敢不阙疑,以俟能言者”.约200年后,祖冲之的儿子祖暅提出“幂势既同,则积不容异”,后世称为祖暅原理,即:两等高立体,若在每一等高处的截面积都相等,则两立体体积相等.如图(3)(4),祖暅利用八分之一正方体去掉八分之一牟合方盖后的几何体与长宽高皆为八分之一正方体的边长的倒四棱锥“等幂等积”,计算出牟合方盖的体积,据此可知,牟合方盖的体积与其外切正方体的体积之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com