
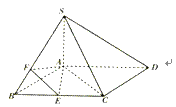
【题目】如图所示,四棱锥S﹣ABCD中,四边形ABCD为平行四边形,BA⊥AC,SA⊥AD,SC⊥CD.
(Ⅰ)求证:AC⊥SB;
(Ⅱ)若AB=AC=SA=3,E为线段BC的中点,F为线段SB上靠近B的三等分点,求直线SC与平面AEF所成角的正弦值.
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】
(Ⅰ)由线面垂直的判定定理证明AC⊥平面SAB,即可证得AC⊥SB.
(Ⅱ)以AB、AC、AS为x轴y轴z轴建立坐标系,用向量法求解即可.
(Ⅰ)∵四边形ABCD为平行四边形,∴BA∥CD,
又BA⊥AC,∴CD⊥AC,
又SC⊥CD,AC∩SC=C,∴CD⊥平面SAC,
又SA平面SAC,∴CD⊥SA,又SA⊥AD,CD∩AD=D,
∴SA⊥平面ABCD,AC平面ABCD,∴SA⊥AC,
又BA⊥AC,SA∩BA=A,∴AC⊥平面SAB,
又SB平面SAB,∴AC⊥SB.
(Ⅱ)以AB、AC、AS为x轴y轴z轴建立如图所示坐标系,
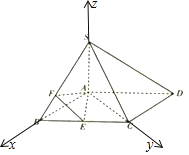
则A(0,0,0),S(0,0,3),C(0,3,0),E(![]() ,
,![]() ,0),F(2,0,1),
,0),F(2,0,1),
∴![]() =(
=(![]() ,
,![]() ,0),
,0),![]() =(2,0,1),
=(2,0,1),![]() =(0,﹣3,3),
=(0,﹣3,3),
设![]() =(x,y,z)为平面AEF的法向量,
=(x,y,z)为平面AEF的法向量,
![]() ,∴
,∴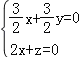 ,∴
,∴![]() ,
,
令x=﹣1,得一个法向量![]() =(﹣1,1,2),
=(﹣1,1,2),
cos<![]() ,
,![]() >=
>=![]() =
=![]() =
=![]()
即直线SC与平面AEF所成角的正弦值为![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】如图,在直角三棱柱![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() .
.
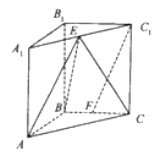
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)若直线![]() 和平面
和平面![]() 所成角的正弦值等于
所成角的正弦值等于![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】①回归分析中,相关指数![]() 的值越大,说明残差平方和越大;
的值越大,说明残差平方和越大;
②对于相关系数![]() ,
,![]() 越接近1,相关程度越大,
越接近1,相关程度越大,![]() 越接近0,相关程度越小;
越接近0,相关程度越小;
③有一组样本数据![]() 得到的回归直线方程为
得到的回归直线方程为![]() ,那么直线
,那么直线![]() 必经过点
必经过点![]() ;
;
④![]() 是用来判断两个分类变量是否有关系的随机变量,只对于两个分类变量适合;
是用来判断两个分类变量是否有关系的随机变量,只对于两个分类变量适合;
以上几种说法正确的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次演唱会上共10 名演员(每名演员都会唱歌或跳舞),其中7人能唱歌,6人会跳舞.
(1)问既能唱歌又会跳舞的有几人?
(2)现要选出一个2人唱歌2人伴舞的节目,有多少种选派方法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:
连续剧 | 连续剧播放时长/min | 广告播放时长/min | 收视人次/万人 |
甲 | 70 | 5 | 60 |
乙 | 60 | 5 | 25 |
电视台每周安排的甲、乙连续剧的总播放时长不多于![]() ,广告的总播放时长不少于
,广告的总播放时长不少于![]() ,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍,分别用
,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍,分别用![]() ,
,![]() 表示每周计划播出的甲、乙两套连续剧的次数,要使总收视人次最多,则电视台每周播出甲、乙两套连续剧的次数分别为( )
表示每周计划播出的甲、乙两套连续剧的次数,要使总收视人次最多,则电视台每周播出甲、乙两套连续剧的次数分别为( )
A.6,3B.5,2C.4,5D.2,7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对函数![]() (其中
(其中![]() 为实数,
为实数,![]() ),给出下列命题;
),给出下列命题;
①当![]() 时,
时,![]() 在定义域上为单调递减函数;②对任意
在定义域上为单调递减函数;②对任意![]() ,
,![]() 都不是奇函数;③当
都不是奇函数;③当![]() 时,
时,![]() 为偶函数;④关于
为偶函数;④关于![]() 的方程
的方程![]() 最多有一个实数根,其中正确命题的序号为________,(把所有正确的命题序号写入横线)
最多有一个实数根,其中正确命题的序号为________,(把所有正确的命题序号写入横线)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]()
![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() ,
,![]() 的公共点为
的公共点为![]() .
.
(Ⅰ)求直线![]() 的斜率;
的斜率;
(Ⅱ)若点![]() 分别为曲线
分别为曲线![]() ,
,![]() 上的动点,当
上的动点,当![]() 取最大值时,求四边形
取最大值时,求四边形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com