
 +
+ =1(a>b>0),称圆心在坐标原点O,半径为
=1(a>b>0),称圆心在坐标原点O,半径为 的圆是椭圆C的“伴随圆”. 若椭圆C的一个焦点为F2(
的圆是椭圆C的“伴随圆”. 若椭圆C的一个焦点为F2( ,0),其短轴上的一个端点到F2距离为
,0),其短轴上的一个端点到F2距离为 .
. ,求m的值;
,求m的值;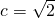 ,a=
,a= ,∴b2=a2-c2=1.
,∴b2=a2-c2=1. ,
,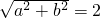 ;
; ,
, ,
,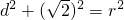 ,∴d2=2,∴m2=2(1+k2).(*)
,∴d2=2,∴m2=2(1+k2).(*)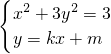 得(1+3k2)x2+6mkx+3m2-3=0,
得(1+3k2)x2+6mkx+3m2-3=0,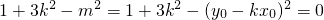 ,
,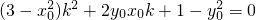 ,∴
,∴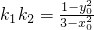 ,
,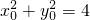 ,∴
,∴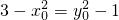 .
. 、及直线与椭圆相切的性质即可得出;
、及直线与椭圆相切的性质即可得出; 、及直线与椭圆相切的性质、“伴椭圆”的定义是解题的关键.
、及直线与椭圆相切的性质、“伴椭圆”的定义是解题的关键. 

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| a2+b2 |
| 2 |
| 3 |
| AB |
| AD |
查看答案和解析>>
科目:高中数学 来源: 题型:
| MA |
| AN |
| MB |
| BN |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省温州市十校联合体高三(上)期末数学试卷(文科)(解析版) 题型:解答题
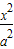 +
+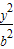 =1(a>b>0),称圆心在坐标原点O,半径为
=1(a>b>0),称圆心在坐标原点O,半径为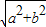 的圆是椭圆C的“伴随圆”. 若椭圆C的一个焦点为F2(
的圆是椭圆C的“伴随圆”. 若椭圆C的一个焦点为F2(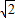 ,0),其短轴上的一个端点到F2距离为
,0),其短轴上的一个端点到F2距离为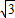 .
.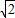 ,求m的值;
,求m的值;查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省济宁市邹城一中高三(上)期末数学模拟试卷(理科)(解析版) 题型:解答题
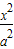 +
+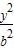 =1(a>b>0),称圆心在坐标原点O,半径为
=1(a>b>0),称圆心在坐标原点O,半径为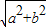 的圆是椭圆C的“伴随圆”. 若椭圆C的一个焦点为F2(
的圆是椭圆C的“伴随圆”. 若椭圆C的一个焦点为F2(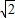 ,0),其短轴上的一个端点到F2距离为
,0),其短轴上的一个端点到F2距离为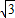 .
.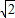 ,求m的值;
,求m的值;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com