
分析 (Ⅰ)求出f(x)的导数,求得单调区间和极值,也为最值;
(Ⅱ)由(Ⅰ)可知$\frac{1}{{e}^{x}}$≤$\frac{1}{x+1}$,令x=n可得$\frac{1}{{e}^{n}}$<$\frac{1}{n+1}$,即为$\frac{1}{n{e}^{n}}$<$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,运用累加法,即可得证;
(Ⅲ)由题意可得f(b)-mb<f(a)-ma,即有函数$h(x)=f(x)-mx=\frac{x+1}{e^x}-mx在({-1,0})$上是减函数,求出导数h′(x)≤0在(-1,0)恒成立,求出导数,可得最大值,即可得到所求m的最小值.
解答 解:(Ⅰ)函数$f(x)=\frac{x+1}{e^x}$的导数为$f'(x)=-\frac{x}{e^x}$,
当x<0,f'(x)>0,f(x)递增;
x>0,f'(x)<0,f(x)递减.
即有x=0处取得最大值,即f(x)≤f(0)=1,
∴f(x)max=1;
(Ⅱ)证明:由(1)知,$\frac{x+1}{e^x}≤1,令x=n({n∈{N_+}})$,
$\frac{1}{e^n}<\frac{1}{n+1}∴\frac{1}{{n{e^n}}}<\frac{1}{{n({n+1})}}=\frac{1}{n}-\frac{1}{n+1}$,
则$\sum_{i=1}^n{\frac{1}{{i{e^i}}}<({1-\frac{1}{2}})+({\frac{1}{2}-\frac{1}{3}})+…+({\frac{1}{n}-\frac{1}{n+1}})}=1-\frac{1}{n+1}=\frac{n}{n+1}$;
(Ⅲ)当$-1<a<b<0时,\frac{f(b)-f(a)}{b-a}<m?f(b)-mb<f(a)-ma$,
即函数$h(x)=f(x)-mx=\frac{x+1}{e^x}-mx在({-1,0})$上是减函数,$?x∈({-1,+∞}),h'(x)=-\frac{x}{e^x}-m≤0,即m≥-\frac{x}{e^x}$,
$u(x)=-\frac{x}{e^x},u'(x)=\frac{x-1}{e^x}$,
当x∈(-1,1),u′(x)<0,u(x)递减;
x∈(1,+∞),u′(x)>0,u(x)递增.
则$u{(x)_{min}}=u(1)=-\frac{1}{e},x→+∞,u(x)=-\frac{x}{e^x}→0$,
u(x)<u(-1)=e,
所以m≥e,即m的最小值为e.
点评 本题考查导数的运用:求单调区间、极值和最值,考查不等式的证明,注意运用累加法和裂项相消求和,考查不等式恒成立问题的解法,注意运用函数的单调性和导数,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$ | B. | -4$\sqrt{3}$ | C. | ±4$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
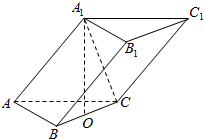 如图,在三棱柱ABC-A1B1C1中,已知A1在底面ABC内的射影是线段BC的中点,且A1O=OC,BC⊥AA1.
如图,在三棱柱ABC-A1B1C1中,已知A1在底面ABC内的射影是线段BC的中点,且A1O=OC,BC⊥AA1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{19}$ | B. | $2\sqrt{6}$ | C. | $\sqrt{34}$ | D. | $\sqrt{39}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 外语 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 8 | m | 9 |
| 良 | 9 | n | 11 | |
| 及格 | 8 | 9 | 11 | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com