
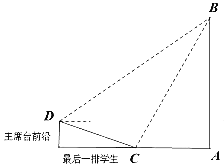
【题目】如图,学校升旗仪式上,主持人站在主席台前沿D处,测得旗杆AB顶部的仰角为![]() 俯角最后一排学生C的俯角为
俯角最后一排学生C的俯角为![]() 最后一排学生C测得旗杆顶部的仰角为
最后一排学生C测得旗杆顶部的仰角为![]() 旗杆底部与学生在一个水平面上,并且不计学生身高.
旗杆底部与学生在一个水平面上,并且不计学生身高.
(1)设![]() 米,试用
米,试用![]() 和
和![]() 表示旗杆的高度AB(米);
表示旗杆的高度AB(米);
(2)测得![]() 米,
米,![]() 若国歌长度约为50秒,国旗班升旗手应以多大的速度匀速升旗才能是国旗到达旗杆顶点时师生的目光刚好停留在B处?
若国歌长度约为50秒,国旗班升旗手应以多大的速度匀速升旗才能是国旗到达旗杆顶点时师生的目光刚好停留在B处?
 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。

(Ⅰ)将y表示为x的函数;
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
求分数在[120,130)内的频率,并补全这个频
率分布直方图;
统计方法中,同一组数据常用该组区间的中点
值作为代表,据此估计本次考试的平均分;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段[120,130)内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知有限集合![]() ,定义如下操作过程
,定义如下操作过程![]() :从
:从![]() 中任取两个元素
中任取两个元素![]() 、
、![]() ,由
,由![]() 中除了
中除了![]() 、以外的元素构成的集合记为
、以外的元素构成的集合记为![]() ;①若
;①若 ,则令
,则令 ;②若
;②若 ,则
,则![]() ;这样得到新集合
;这样得到新集合![]() ,例如集合
,例如集合![]() 经过一次操作后得到的集合可能是
经过一次操作后得到的集合可能是![]() 也可能得到
也可能得到![]() 等,可继续对取定的
等,可继续对取定的![]() 实施操作过程
实施操作过程![]() ,得到的新集合记作
,得到的新集合记作![]() ,……,如此经过
,……,如此经过![]() 次操作后得到的新集合记作
次操作后得到的新集合记作![]() ,设
,设![]() ,对于
,对于![]() ,反复进行上述操作过程,当所得集合
,反复进行上述操作过程,当所得集合![]() 只有一个元素时,则所有可能的集合
只有一个元素时,则所有可能的集合![]() 为______.
为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
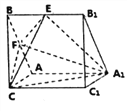
【题目】已知正三棱柱![]() 中,
中, ![]() 分别为
分别为![]() 的中点,设
的中点,设![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的平面角为
的平面角为![]() ,求实数
,求实数![]() 的值,并判断此时二面角
的值,并判断此时二面角![]() 是否为直二面角,请说明理由.
是否为直二面角,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 为向国际化大都市目标迈进,沈阳市今年新建三大类重点工程,它们分别是30项基础设施类工程,20项民生类工程和10项产业建设类工程.现有来沈阳的3名工人相互独立地从这60个项目中任选一个项目参与建设.
(Ⅰ)求这3人选择的项目所属类别互异的概率;
(Ⅱ)将此3人中选择的项目属于基础设施类工程或产业建设类工程的人数记为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com