
 BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).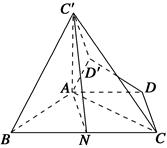
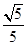
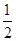 BC,N是BC的中点,∴AD=NC,又AD∥BC,∴四边形ANCD是平行四边形,∴AN=DC,又∠ABC=60°,∴AB=BN=AD,
BC,N是BC的中点,∴AD=NC,又AD∥BC,∴四边形ANCD是平行四边形,∴AN=DC,又∠ABC=60°,∴AB=BN=AD,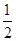 ∠DCB=30°,
∠DCB=30°,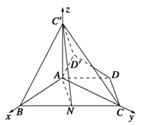
 ,0),C′(0,0,
,0),C′(0,0, ),
),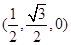 ,∴
,∴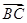 ′=(-1,0,
′=(-1,0, ),
),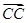 ′=(0,-
′=(0,- ,
, ),设平面C′NC的法向量为n=(x,y,z),则
),设平面C′NC的法向量为n=(x,y,z),则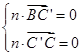 即
即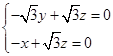
 ,y=1,∴n=(
,y=1,∴n=( ,1,1).
,1,1).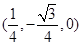 ,∴平面C′AN的法向量
,∴平面C′AN的法向量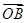 =
=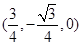 .
.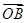 〉=
〉=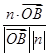 =
=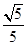 ,
,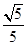


科目:高中数学 来源:不详 题型:解答题
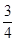 BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4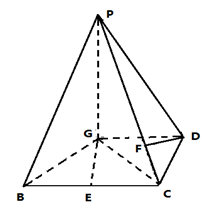
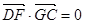 ,
,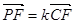 ,求
,求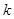 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
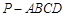 的底面
的底面 是直角梯形,
是直角梯形,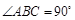 ,
,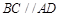 ,且
,且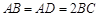 ,顶点
,顶点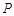 在底面
在底面 内的射影恰好落在
内的射影恰好落在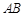 的中点
的中点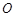 上.
上.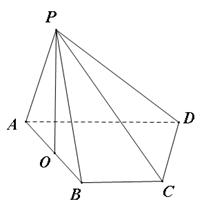
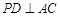 ;
;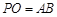 ,求直线
,求直线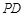 与
与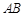 所成角的 余弦值;
所成角的 余弦值;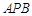 与平面
与平面 所成的二面角为
所成的二面角为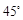 ,求
,求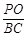 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
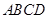 为直角梯形,
为直角梯形,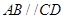 ,
,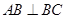 ,
,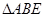 为等边三角形,且平面
为等边三角形,且平面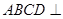 平面
平面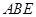 ,
,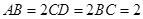 ,
,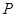 为
为 中点.
中点.
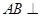
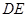 ;
;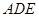 与平面
与平面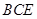 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;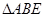 内是否存在一点
内是否存在一点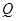 ,使
,使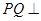 平面
平面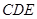 ,如果存在,求
,如果存在,求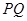 的长;如果不存在,说明理由.
的长;如果不存在,说明理由. 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
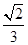 a,则MN与平面BB1C1C的位置关系是________.
a,则MN与平面BB1C1C的位置关系是________.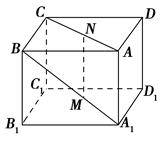
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com