
【题目】在三棱锥P﹣ABC中,AB=1,BC=2,AC![]() ,PC
,PC![]() ,PA
,PA![]() ,PB
,PB![]() ,E是线段BC的中点.
,E是线段BC的中点.
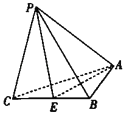
(1)求点C到平面APE的距离d;
(2)求二面角P﹣EA﹣B的余弦值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)建立空间直角坐标系,求出平面![]() 的法向量,利用向量的距离公式得解;(2)求出两个平面的法向量,利用向量公式求解.
的法向量,利用向量的距离公式得解;(2)求出两个平面的法向量,利用向量公式求解.
∵AB2+BC2=AC2,PC2+BC2=PB2,PA2+AB2=PB2,
∴![]() ,
,
过点P作PO⊥平面ABC,垂足为O,易得OP=1,且BC⊥OC,BA⊥OA,
∴四边形ABCO为矩形,
(1)以O为坐标原点,建立如图所示的空间直角坐标系,
则C(1,0,0),E(1,1,0),A(0,2,0),P(0,0,1),
![]() ,
,
设平面APE的法向量为![]() ,则
,则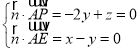 ,
,
令x=1,则![]() ,
,
∴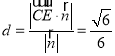 ;
;
(2)由(1)知平面APE的法向量为![]() ,取平面ABE的一个法向量
,取平面ABE的一个法向量![]() ,
,
且二面角P﹣EA﹣B为钝角,设其为θ,故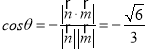 .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.

(Ⅰ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(Ⅱ)当二面角![]() 的余弦值为
的余弦值为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一枚质地均匀的硬币连掷三次,事件“恰出现1次反面朝上”的概率记为![]() ,现采用随机模拟的方法估计
,现采用随机模拟的方法估计![]() 的值:用计算机产生了20组随机数,其中出现“0”表示反面朝上,出现“1”表示正面朝上,结果如下,若出现“恰有1次反面朝上”的频率记为
的值:用计算机产生了20组随机数,其中出现“0”表示反面朝上,出现“1”表示正面朝上,结果如下,若出现“恰有1次反面朝上”的频率记为![]() ,则
,则![]() ,
,![]() 分别为( )
分别为( )
111 001 011 010 000 111 111 111 101 010
000 101 011 010 001 011 100 101 001 011
A. ![]() ,
,![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 是双曲线
是双曲线![]() :
:![]() 的左右焦点,其渐近线为
的左右焦点,其渐近线为![]() ,且右顶点到左焦点的距离为3.
,且右顶点到左焦点的距离为3.
(1)求双曲线![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 、
、![]() 两点,直线
两点,直线![]() 的法向量为
的法向量为![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若双曲线![]() 在第四象限的部分存在一点
在第四象限的部分存在一点![]() 满足
满足![]() ,求
,求![]() 的值及
的值及![]() 的面积
的面积![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A是圆O:x2+y2=16上的任意一点,l是过点A且与x轴垂直的直线,B是直线l与x轴的交点,点Q在直线l上,且满足4|BQ|=3|BA|.当点A在圆O上运动时,记点Q的轨迹为曲线C.
(1)求曲线C的方程;
(2)已知直线y=kx﹣2(k≠0)与曲线C交于M,N两点,点M关于y轴的对称点为M′,设P(0,﹣2),证明:直线M′N过定点,并求△PM′N面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电力公司在工程招标中是根据技术、商务、报价三项评分标准进行综合评分的,按照综合得分的高低进行综合排序,综合排序高者中标.
分值权重表如下:
总分 | 技术 | 商务 | 报价 |
100% | 50% | 10% | 40% |
技术标、商务标基本都是由公司的技术、资质、资信等实力来决定的.报价表则相对灵活,报价标的评分方法是:基准价的基准分是68分,若报价每高于基准价1%,则在基准分的基础上扣0.8分,最低得分48分;若报价每低于基准价1%,则在基准分的基础上加0.8分,最高得分为80分.若报价低于基准价15%以上(不含15%)每再低1%,在80分在基础上扣0.8分.
在某次招标中,若基准价为1000(万元).甲、乙两公司综合得分如下表:
公司 | 技术 | 商务 | 报价 |
甲 | 80分 | 90分 | A甲分 |
乙 | 70分 | 100分 | A乙分 |
甲公司报价为1100(万元),乙公司的报价为800(万元)则甲,乙公司的综合得分,分别是( )
A. 73,75.4B. 73,80C. 74.6,76D. 74.6,75.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:对于实数![]() 和两定点
和两定点![]() ,在某图形上恰有
,在某图形上恰有![]() 个不同的点
个不同的点![]() ,使得
,使得![]() ,称该图形满足“
,称该图形满足“![]() 度契合”.若边长为4的正方形
度契合”.若边长为4的正方形![]() 中,
中,![]() ,且该正方形满足“4度契合”,则实数
,且该正方形满足“4度契合”,则实数![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com