
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .现将
.现将![]() 沿
沿![]() 翻折至
翻折至![]() ,得四棱锥.
,得四棱锥.![]()
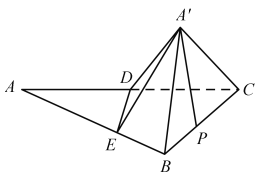
(1)证明:![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正切值
所成角的正切值
【答案】(1)证明见解析;(2)7
【解析】
(1)设![]() 为
为![]() 的中点,通过证明
的中点,通过证明![]() ,
,![]() 来证明
来证明![]() 面
面![]() ,从而证得
,从而证得![]() ;
;
(2)法一:连结![]() ,设
,设![]() 在面
在面![]() 上的射影点为
上的射影点为![]() ,则由题知点
,则由题知点![]() 在
在![]() 上,且
上,且![]() 为直线
为直线![]() 与平面
与平面![]() 所成角,通过条件算出
所成角,通过条件算出![]() ,
,![]() ,即可求得直线
,即可求得直线![]() 与平面
与平面![]() 所成角的正切值;
所成角的正切值;
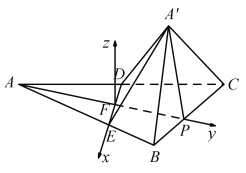
法二:如图,以![]() 为原点,
为原点,![]() 为
为![]() 轴建立空间直角坐标系,运用向量法求解直线
轴建立空间直角坐标系,运用向量法求解直线![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.
(1)设![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() ,则
,则![]() ,
,
故![]() ,则
,则![]() ,
,
又![]() ,则
,则![]() ,
,
所以![]() 是
是![]() 的角平分线,且
的角平分线,且![]() 三点共线.
三点共线.
由![]() ,且
,且![]() ,得
,得![]() 面
面![]() ,则
,则![]() ;
;
(2)法一:连结![]() .
.
由![]() 平面
平面![]() 得,平面
得,平面![]() 平面
平面![]() ,交线为
,交线为![]() ,
,
所以![]() 在面
在面![]() 上的射影点
上的射影点![]() 在
在![]() 上,
上,
![]() 为直线
为直线![]() 与平面
与平面![]() 所成角.
所成角.
在![]() 中,
中,![]() ,由余弦定理得
,由余弦定理得![]() ,
,
![]() ,故
,故![]() ,
,![]() ,
,
又![]() ,在
,在![]() 得,由余弦定理得
得,由余弦定理得![]() ,则
,则![]() ,
,
所以![]() ,
,
由(1)得![]() 为角平分线,
为角平分线,
在![]() 中,
中,![]() ,由余弦定理得
,由余弦定理得![]() ,则
,则![]() ,所以
,所以
![]() ,所以直线
,所以直线![]() 与平面
与平面![]() 所成角的正切值为7.
所成角的正切值为7.
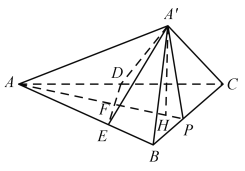
法二:如图,以![]() 为原点,
为原点,![]() 为
为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
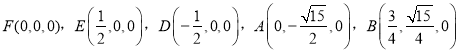 ,
,

设![]() ,由
,由![]() ,
,![]() 得
得
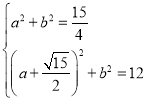 ,
,
得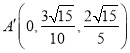 .
.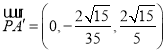 ,
,
平面![]() 法向量为
法向量为![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,所以
,所以
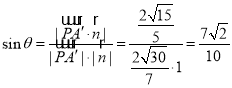 ,
,![]() ,则
,则![]() ,
,
所以直线![]() 与平面
与平面![]() 所成角的正切值为7.
所成角的正切值为7.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】随机调查某城市80名有子女在读小学的成年人,以研究晚上八点至十点时间段辅导子女作业与性别的关系,得到下面的数据表:
是否辅导 性别 | 辅导 | 不辅导 | 合计 |
男 | 25 | 60 | |
女 | |||
合计 | 40 | 80 |
(1)请将表中数据补充完整;
(2)用样本的频率估计总体的概率,估计这个城市有子女在读小学的成人女性晚上八点至十点辅导子女作业的概率;
(3)根据以上数据,能否有99%以上的把握认为“晚上八点至十点时间段是否辅导子女作业与性别有关?”.
参考公式: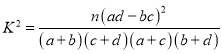 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】羽毛球比赛中,首局比赛由裁判员采用抛球的方法决定谁先发球,在每回合争夺中,赢方得1分且获得发球权.每一局中,获胜规则如下:①率先得到21分的一方赢得该局比赛;②如果双方得分出现![]() ,需要领先对方2分才算该局获胜;③如果双方得分出现
,需要领先对方2分才算该局获胜;③如果双方得分出现![]() ,先取得30分的一方该局获胜.现甲、乙两名运动员进行对抗赛,在每回合争夺中,若甲发球时,甲得分的概率为
,先取得30分的一方该局获胜.现甲、乙两名运动员进行对抗赛,在每回合争夺中,若甲发球时,甲得分的概率为![]() ;乙发球时,甲得分的概率为
;乙发球时,甲得分的概率为![]() .
.
(Ⅰ)若![]() ,记“甲以
,记“甲以![]() 赢一局”的概率为
赢一局”的概率为![]() ,试比较
,试比较![]() 与
与![]() 的大小;
的大小;
(Ⅱ)根据对以往甲、乙两名运动员的比赛进行数据分析,得到如下![]() 列联表部分数据.若不考虑其它因素对比赛的影响,并以表中两人发球时甲得分的频率作为
列联表部分数据.若不考虑其它因素对比赛的影响,并以表中两人发球时甲得分的频率作为![]() ,
,![]() 的值.
的值.
甲得分 | 乙得分 | 总计 | |
甲发球 | 50 | 100 | |
乙发球 | 60 | 90 | |
总计 | 190 |
①完成![]() 列联表,并判断是否有95%的把握认为“比赛得分与接、发球有关”?
列联表,并判断是否有95%的把握认为“比赛得分与接、发球有关”?
②已知在某局比中,双方战成![]() ,且轮到乙发球,记双方再战
,且轮到乙发球,记双方再战![]() 回合此局比赛结束,求
回合此局比赛结束,求![]() 的分布列与期望.
的分布列与期望.
参考公式: ,其中
,其中![]() .
.
临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() 离心率
离心率![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)经过椭圆左焦点![]() 的直线(不经过点
的直线(不经过点![]() 且不与
且不与![]() 轴重合)与椭圆交于
轴重合)与椭圆交于![]() 两点,与直线
两点,与直线![]() :
:![]() 交于点
交于点![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() .则是否存在常数
.则是否存在常数![]() ,使得向量
,使得向量![]()
![]() 共线?若存在求出
共线?若存在求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,新型冠状病毒肺炎(COVID-19)在我国爆发,全国人民团结一心、积极抗疫,为全世界疫情防控争取了宝贵的时间,积累了丰富的经验.某研究小组为了研究某城市肺炎感染人数的增长情况,在官方网站.上搜集了7组数据,并依据数据制成如下散点图:
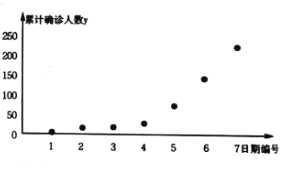
图中![]() 表示日期代号(例如2月1日记为“1”,2月2日记为“2”,以此类推).通过对散点图的分析,结合病毒传播的相关知识,该研究小组决定用指数型函数模型
表示日期代号(例如2月1日记为“1”,2月2日记为“2”,以此类推).通过对散点图的分析,结合病毒传播的相关知识,该研究小组决定用指数型函数模型![]() 来拟合,为求出
来拟合,为求出![]() 关于
关于![]() 的回归方程,可令
的回归方程,可令![]() ,则
,则![]() 与
与![]() 线性相关.初步整理后,得到如下数据:
线性相关.初步整理后,得到如下数据:![]() ,
,![]() .
.
(1)根据所给数据,求出![]() 关于
关于![]() 的线性回归方程:
的线性回归方程:
(2)求![]() 关于
关于![]() 的回归方程;若防控不当,请问
的回归方程;若防控不当,请问![]() 为何值时,累计确诊人数的预报值将超过1000人?(参考数据:
为何值时,累计确诊人数的预报值将超过1000人?(参考数据:![]() ,结果保留整数)
,结果保留整数)
附:对于一组数据![]() ,其线性回归方程
,其线性回归方程![]() 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为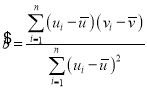 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全面抗击新冠肺炎疫情这一特殊时期,我市教育局提出“停课不停学”的口号,鼓励学生线上学习.某校数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系,对高三年级随机选取45名学生进行跟踪问卷,其中每周线上学习数学时间不少于5小时的有19人,余下的人中,在检测考试中数学平均成绩不足120分的占![]() ,统计成绩后得到如下
,统计成绩后得到如下![]() 列联表:
列联表:
分数不少于120分 | 分数不足120分 | 合计 | |
线上学习时间不少于5小时 | 4 | 19 | |
线上学习时间不足5小时 | |||
合计 | 45 |
(1)请完成上面![]() 列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
(2)①按照分层抽样的方法,在上述样本中从分数不少于120分和分数不足120分的两组学生中抽取9名学生,设抽到不足120分且每周线上学习时间不足5小时的人数是![]() ,求
,求![]() 的分布列(概率用组合数算式表示);
的分布列(概率用组合数算式表示);
②若将频率视为概率,从全校高三该次检测数学成绩不少于120分的学生中随机抽取20人,求这些人中每周线上学习时间不少于5小时的人数的期望和方差.
(下面的临界值表供参考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式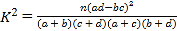 其中
其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C的对边长分别等于a,b,c,列举如下五个条件:①![]() ;②
;②![]() ;③cosA+cos2A=0;④a=4;⑤△ABC的面积等于
;③cosA+cos2A=0;④a=4;⑤△ABC的面积等于![]() .
.
(1)请在五个条件中选择一个(只需选择一个)能够确定角A大小的条件来求角A;
(2)在(1)的结论的基础上,再在所给条件中选择一个(只需选择一个),求△ABC周长的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强学生的冬奥会知识,弘扬奥林匹克精神,北京市多所中小学校开展了模拟冬奥会各项比赛的活动.为了了解学生在越野滑轮和旱地冰壶两项中的参与情况,在北京市中小学学校中随机抽取了10所学校,10所学校的参与人数如下:
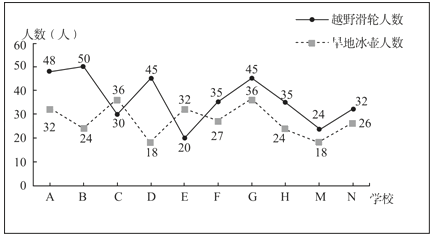
(Ⅰ)现从这10所学校中随机选取2所学校进行调查.求选出的2所学校参与越野滑轮人数都超过40人的概率;
(Ⅱ)现有一名旱地冰壶教练在这10所学校中随机选取2所学校进行指导,记X为教练选中参加旱地冰壶人数在30人以上的学校个数,求X的分布列和数学期望;
(Ⅲ)某校聘请了一名越野滑轮教练,对高山滑降、转弯、八字登坡滑行这3个动作进行技术指导.规定:这3个动作中至少有2个动作达到“优”,总考核记为“优”.在指导前,该校甲同学3个动作中每个动作达到“优”的概率为0.1.在指导后的考核中,甲同学总考核成绩为“优”.能否认为甲同学在指导后总考核达到“优”的概率发生了变化?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,五边形![]() 中,四边形
中,四边形![]() 为长方形,
为长方形,![]() 为边长为
为边长为![]() 的正三角形,将
的正三角形,将![]() 沿
沿![]() 折起,使得点
折起,使得点![]() 在平面
在平面![]() 上的射影恰好在
上的射影恰好在![]() 上.
上.
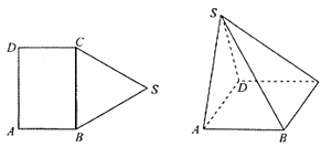
(Ⅰ)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成二面角的余弦值的绝对值.
所成二面角的余弦值的绝对值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com