
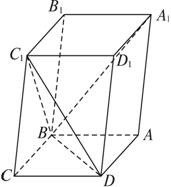
(1)求证:CC1⊥BD;
(2)当![]() 的值为多少时,能使A1C⊥平面C1BD?并加以证明.
的值为多少时,能使A1C⊥平面C1BD?并加以证明.
思路解析:在平行六面体中,通常以同一顶点上三条棱所在的直线的方向向量为基向量,建立空间向量基底.
(1)证明:取![]() =a,
=a,![]() =b,
=b,![]() =c为空间的一个基底,设菱形的边长为a.
=c为空间的一个基底,设菱形的边长为a.
∵![]() =a-b,∴
=a-b,∴![]() ·
·![]() =c·a-c·b=|c||a|cos〈c,a〉-|c||b|cos〈c,b〉=|c|acos60°-|c|acos60°=0.
=c·a-c·b=|c||a|cos〈c,a〉-|c||b|cos〈c,b〉=|c|acos60°-|c|acos60°=0.
∴![]() ⊥
⊥![]() .∴
.∴![]() ⊥
⊥![]() .
.
(2)设![]() =λ(λ>0),即|
=λ(λ>0),即|![]() |=λ|
|=λ|![]() |时,能使A
|时,能使A
∵C1D![]() 平面BC1D,BD
平面BC1D,BD![]() 平面BC1D,∴A
平面BC1D,∴A
∴![]() ·
·![]() =0且
=0且![]() ·
·![]() =0.
=0.
∵![]() =-(a+b+c),
=-(a+b+c), ![]() =a-c,〈a,b〉=〈b,c〉=60°,|a|=|b|=a,
=a-c,〈a,b〉=〈b,c〉=60°,|a|=|b|=a,
∴![]() ·
·![]() =-(a+b+c)·(a-c)=-a2-aacos60°+a·
=-(a+b+c)·(a-c)=-a2-aacos60°+a·![]() cos60°+
cos60°+![]()
∴3λ2-λ-2=0.∵λ>0,∴λ=1.
当λ=1时,
![]() ·
·![]() =-(a+b+c)·(a-b)=-a2+a2-aacos60°+aacos60°=0,
=-(a+b+c)·(a-b)=-a2+a2-aacos60°+aacos60°=0,
∴![]() ⊥
⊥![]() .∴A
.∴A
同理,当λ=1时,![]() ⊥
⊥![]() ,即A
,即A
由上述证明过程知当![]() 时,能使A
时,能使A
方法归纳 向量法解决线面垂直问题时,通常转化为此直线的方向向量垂直于平面内两不共线的向量问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
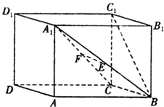 如图所示,已知直平行六面体ABCD-A1B1C1D1的底面边长均为2a,侧棱长为a,∠ABC=60°,E、F分别是A1B、A1C的中点.
如图所示,已知直平行六面体ABCD-A1B1C1D1的底面边长均为2a,侧棱长为a,∠ABC=60°,E、F分别是A1B、A1C的中点.查看答案和解析>>
科目:高中数学 来源:高考零距离 二轮冲刺优化讲练 数学 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源:单元双测 同步达标活页试卷 高二数学(下A) 人教版 题型:047
| |||||||||||||||
查看答案和解析>>
科目:高中数学 来源:同步题 题型:证明题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com