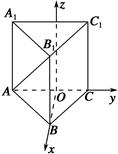
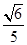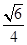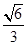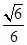如图,
ABCD是块矩形硬纸板,其中
AB=2
AD,
AD=
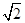
,
E为
DC的中点,将它沿
AE折成直二面角
D-AE-B.
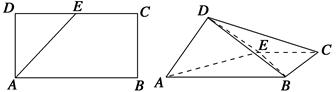
(1)求证:
AD⊥平面
BDE;
(2)求二面角
B-AD-E的余弦值.
(1)见解析(2)
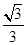
(1)由题设可知
AD⊥
DE,取
AE中点
O,连接
OD,
BE.∵
AD=
DE=
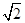
,∴
OD⊥
AE.又二面角
D-AE-B为直二面角,∴
OD⊥平面
ABCE.又
AE=
BE=2,
AB=2
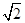
,∴
AB2=
AE2+
BE2.∴
AE⊥
BE.取
AB中点
F,连接
OF,则
OF∥
EB.∴
OF⊥
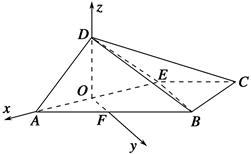
AE.以点
O为原点,
OA,
OF,
OD分别为
x,
y,
z轴建立空间直角坐标系(如图),
则
A(1,0,0),
D(0,0,1),
B(-1,2,0),
E(-1,0,0),
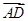
=(-1,0,1),
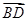
=(1,-2,1),
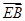
=(0,2,0),
设
n=(
x1,
y1,
z1)是平面
BDE的法向量,
则
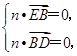
即
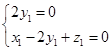
取
x1=1,则
z1=-1.
于是
n=(1,0,-1).∴
n=-
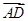
.∴
n∥
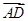
.∴
AD⊥平面
BDE.
(2)设
m=(
x2,
y2,
z2)是平面
ABD的一个法向量,
则
m·
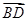
=0,
m·
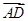
=0,∴
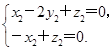
取
x2=1,则
y2=1,
z2=1,则
m=(1,1,1),平面
ADE的法向量
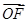
=(0,1,0).∴cos〈
m,
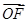
〉=
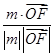
=
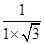
=
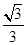
.∴二面角
B-AD-E的余弦值为
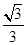
.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
在直三棱柱中,AA
1=AB=BC=3,AC=2,D是AC的中点.
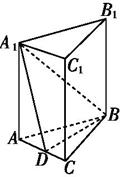
(1)求证:B
1C∥平面A
1BD;
(2)求平面A
1DB与平面DBB
1夹角的余弦值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
在四面体O-ABC中,点P为棱BC的中点.设
=,
=,
=,那么向量
用基底{
,
,
}可表示为( )
| A.-a+b+c | B.-a+b+c |
| C.a+b+c | D.a+b+c |
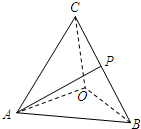
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
下列命题中正确的是( )
| A.若∥,∥,则与所在直线平行 |
| B.向量、、共面即它们所在直线共面 |
| C.空间任意两个向量共面 |
| D.若∥,则存在唯一的实数λ,使=λ |
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
如图所示,在三棱锥
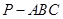
中,
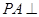
平面
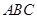
,
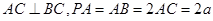
,则
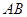
与平面
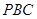
所成角的正弦值为__________.

查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知正三棱柱
ABC-A1B1C1的侧棱长与底面边长相等,则
AB1与侧面
ACC1A1所成角的正弦等于( ).
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
如图,在直三棱柱
ABC-A1B1C1中,∠
ACB=90°,
AA1=2,
AC=
BC=1,则异面直线
A1B与
AC所成角的余弦值是 ( ).
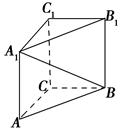
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
如图,正方体

的棱长为

,

、

分别是

、

的中点.

⑴求多面体

的体积;
⑵求

与平面

所成角的余弦值.
查看答案和解析>>

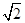 ,E为DC的中点,将它沿AE折成直二面角D-AE-B.
,E为DC的中点,将它沿AE折成直二面角D-AE-B.
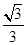
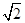 ,∴OD⊥AE.又二面角D-AE-B为直二面角,∴OD⊥平面ABCE.又AE=BE=2,AB=2
,∴OD⊥AE.又二面角D-AE-B为直二面角,∴OD⊥平面ABCE.又AE=BE=2,AB=2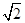 ,∴AB2=AE2+BE2.∴AE⊥BE.取AB中点F,连接OF,则OF∥EB.∴OF⊥AE.以点O为原点,OA,OF,OD分别为x,y,z轴建立空间直角坐标系(如图),
,∴AB2=AE2+BE2.∴AE⊥BE.取AB中点F,连接OF,则OF∥EB.∴OF⊥AE.以点O为原点,OA,OF,OD分别为x,y,z轴建立空间直角坐标系(如图),
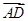 =(-1,0,1),
=(-1,0,1),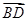 =(1,-2,1),
=(1,-2,1),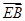 =(0,2,0),
=(0,2,0),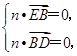 即
即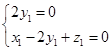 取x1=1,则z1=-1.
取x1=1,则z1=-1. .∴n∥
.∴n∥ .∴AD⊥平面BDE.
.∴AD⊥平面BDE. =0,m·
=0,m·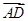 =0,∴
=0,∴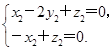 取x2=1,则y2=1,z2=1,则m=(1,1,1),平面ADE的法向量
取x2=1,则y2=1,z2=1,则m=(1,1,1),平面ADE的法向量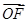 =(0,1,0).∴cos〈m,
=(0,1,0).∴cos〈m,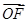 〉=
〉=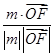 =
=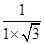 =
=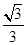 .∴二面角B-AD-E的余弦值为
.∴二面角B-AD-E的余弦值为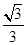 .
.