
思路分析:观察直线与曲线都经过(0,0)点,说明切点可能位于(0,0)点或其他点处,再分类讨论,否则易漏解.
解:∵y=x3-3x2+2x,∴y′=3x2-6x+2.
y′|x0=2,又∵直线与曲线都经过原点,则
①若直线与曲线切于原点时,k=2.
②若直线与曲线切于原点外另一点(x0,y0)(x0≠0)
则k=![]() ,由(x0,y0)在曲线y=x3-3x2+2x上,∴y0=
,由(x0,y0)在曲线y=x3-3x2+2x上,∴y0=![]() +2x0,又∵
+2x0,又∵![]() =k,
=k,
∴有k=![]() =
=![]() -3x0+2,又∵y′=3x2-6x+2,∴k=3
-3x0+2,又∵y′=3x2-6x+2,∴k=3![]() -6x2+2.∴
-6x2+2.∴![]() -3x0+2=3
-3x0+2=3![]() -6x0+2.∴x0=0(舍)或x0=
-6x0+2.∴x0=0(舍)或x0=![]() .所以,当x0=
.所以,当x0=![]() 时,k=(
时,k=(![]() )2-3×
)2-3×![]() +2=-
+2=-![]() .综上所述k=2或k=-
.综上所述k=2或k=-![]() .
.


科目:高中数学 来源:2010年宁夏银川一中高考数学三模试卷(文科)(解析版) 题型:解答题
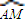 =2
=2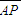 ,
,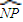 •
•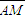 =0,点N的轨迹为曲线E.
=0,点N的轨迹为曲线E.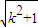 与(1)中所求点N的轨迹E交于不同两点F,H,O是坐标原点,且
与(1)中所求点N的轨迹E交于不同两点F,H,O是坐标原点,且 ≤
≤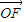 •
•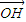 ≤
≤ ,求k2的取值范围.
,求k2的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com