
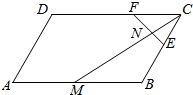
 ČįÍžÆ―ÐÐËÄąßÐÎABCDÖÐĢŽ$\overrightarrow{AB}$=$\overrightarrow{b}$ĢŽ$\overrightarrow{AD}$=$\overrightarrow{d}$ĢŽFĘĮCDĩÄČýĩČ·ÖĩãĢŽEĘĮBCÖÐĩãĢŽMĘĮABÖÐĩãĢŽMCĄÉEF=NĢŽČô$\overrightarrow{MN}$=ĶË1$\overrightarrow{b}$+ĶË2$\overrightarrow{d}$ĢŽÔōĶË1+ĶË2=ĢĻĄĄĄĄĢĐ
ČįÍžÆ―ÐÐËÄąßÐÎABCDÖÐĢŽ$\overrightarrow{AB}$=$\overrightarrow{b}$ĢŽ$\overrightarrow{AD}$=$\overrightarrow{d}$ĢŽFĘĮCDĩÄČýĩČ·ÖĩãĢŽEĘĮBCÖÐĩãĢŽMĘĮABÖÐĩãĢŽMCĄÉEF=NĢŽČô$\overrightarrow{MN}$=ĶË1$\overrightarrow{b}$+ĶË2$\overrightarrow{d}$ĢŽÔōĶË1+ĶË2=ĢĻĄĄĄĄĢĐ| AĢŪ | $\frac{15}{14}$ | BĢŪ | 1 | CĢŪ | $\frac{5}{14}$ | DĢŪ | -$\frac{5}{14}$ |
·ÖÎö ĘđÓÃēŧÍŽ·―·ĻÓÃ$\overrightarrow{b}ĢŽ\overrightarrow{d}$ąíĘūģö$\overrightarrow{MN}$ĢŽ―ášÏÆ―ÃæÏōÁŋĩÄŧųąūĩĀĀíÁÐģö·―ģĖ―âģöĢŪ
―âīð ―âĢš$\overrightarrow{MC}$=$\overrightarrow{MB}+\overrightarrow{BC}$=$\frac{1}{2}\overrightarrow{b}+\overrightarrow{d}$ĢŽ$\overrightarrow{EF}=\overrightarrow{EC}+\overrightarrow{CF}$=$\frac{1}{2}\overrightarrow{d}-\frac{1}{3}\overrightarrow{b}$ĢŽ
Éč$\overrightarrow{MN}=k\overrightarrow{MC}$ĢŽ$\overrightarrow{EN}=ĶĖ\overrightarrow{EF}$ĢŽÔō$\overrightarrow{MN}=\frac{k}{2}\overrightarrow{b}+k\overrightarrow{d}$ĢŽ$\overrightarrow{EN}$=$\frac{ĶĖ}{2}\overrightarrow{d}-\frac{ĶĖ}{3}\overrightarrow{b}$ĢŽ
Ąß$\overrightarrow{MN}$=$\overrightarrow{MB}+\overrightarrow{BE}+\overrightarrow{EN}$=$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{d}$+$\frac{ĶĖ}{2}\overrightarrow{d}-\frac{ĶĖ}{3}\overrightarrow{b}$=ĢĻ$\frac{1}{2}-\frac{ĶĖ}{3}$ĢĐ$\overrightarrow{b}$+ĢĻ$\frac{1}{2}+\frac{ĶĖ}{2}$ĢĐ$\overrightarrow{d}$ĢŽ
Ąā$\left\{\begin{array}{l}{\frac{1}{2}-\frac{ĶĖ}{3}=\frac{k}{2}}\\{\frac{1}{2}+\frac{ĶĖ}{2}=k}\end{array}\right.$ĢŽ―âĩÃ$\left\{\begin{array}{l}{ĶĖ=\frac{3}{7}}\\{k=\frac{5}{7}}\end{array}\right.$ĢŪ
ĄāĶË1+ĶË2=$\frac{k}{2}+k$=$\frac{15}{14}$ĢŪ
đĘŅĄAĢŪ
ĩãÆĀ ąūĖâŋžēéÁËÆ―ÃæÏōÁŋĩÄŧųąūĩĀĀíž°ÆäŌâŌåĢŽÓÃ$\overrightarrow{b}ĢŽ\overrightarrow{d}$ąíĘūģö$\overrightarrow{MN}$ĘĮđØžüĢŪ


 ÔÄķÁŋėģĩÏĩÁÐīð°ļ
ÔÄķÁŋėģĩÏĩÁÐīð°ļ
| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢšŅĄÔņĖâ
| AĢŪ | $\frac{\sqrt{10}}{4}$ | BĢŪ | $\frac{\sqrt{6}}{4}$ | CĢŪ | $\frac{\sqrt{2}}{4}$ | DĢŪ | -$\frac{\sqrt{10}}{4}$ |
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš―âīðĖâ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢšĖîŋÕĖâ
 ČįÍžĢŽĩãOΊŨũžōÐģÕņķŊĩÄÎïĖåĩÄÆ―šâÎŧÖÃĢŽČĄÏōÓŌ·―ÏōΊÕý·―ÏōĢŽČôÕņ·ųΊ3cmĢŽÖÜÆÚΊ4sĢŽĮŌÎïĖåÏōÓŌÔËķŊĩ―ūāÆ―šâÎŧÖÃŨîÔķīĶĘąŋŠĘžžÆĘąĢŪÔōļÃÎïĖå10sĘąŋĖĩÄ·ģĖΊ-3cmĢŪ
ČįÍžĢŽĩãOΊŨũžōÐģÕņķŊĩÄÎïĖåĩÄÆ―šâÎŧÖÃĢŽČĄÏōÓŌ·―ÏōΊÕý·―ÏōĢŽČôÕņ·ųΊ3cmĢŽÖÜÆÚΊ4sĢŽĮŌÎïĖåÏōÓŌÔËķŊĩ―ūāÆ―šâÎŧÖÃŨîÔķīĶĘąŋŠĘžžÆĘąĢŪÔōļÃÎïĖå10sĘąŋĖĩÄ·ģĖΊ-3cmĢŪēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš―âīðĖâ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢšŅĄÔņĖâ
| AĢŪ |  | BĢŪ |  | CĢŪ |  | DĢŪ |  |
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢšŅĄÔņĖâ
| AĢŪ | ģä·ÖķøēŧąØŌŠĖõžþ | BĢŪ | ąØŌŠķøēŧģä·ÖĖõžþ | ||
| CĢŪ | ģäŌŠĖõžþ | DĢŪ | žČēŧģä·ÖŌēēŧąØŌŠĖõžþ |
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢšĖîŋÕĖâ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš―âīðĖâ
ēéŋīīð°ļšÍ―âÎö>>
°ŲķČÖÂÐÅ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com