
【题目】设函数![]() 是定义域为
是定义域为![]() 的奇函数.
的奇函数.
(1)若![]() ,求使不等式
,求使不等式![]() 对一切
对一切![]() 恒成立的实数
恒成立的实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 的图象过点
的图象过点![]() ,是否存在正数
,是否存在正数![]() ,使函数
,使函数![]() 在
在![]() 上的最大值为0?若存在,求出
上的最大值为0?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)由f(1)>0得a![]() 又a>0,求出a>1,判断函数的单调性f(x)=ax﹣a﹣x为R上的增函数,不等式整理为x2﹣(k+1)x+1>0对一切x∈R恒成立,利用判别式法求解即可;
又a>0,求出a>1,判断函数的单调性f(x)=ax﹣a﹣x为R上的增函数,不等式整理为x2﹣(k+1)x+1>0对一切x∈R恒成立,利用判别式法求解即可;
(2)把点代入求出a=2,假设存在正数m,构造函数设s=2x﹣2﹣x则(2x﹣2﹣x)2﹣m(2x﹣2﹣x)+2=s2﹣ms+2,对底数m进行分类讨论,判断m的值.
(1) ![]() ,由
,由![]() 得
得 ![]() ,又
,又 ![]() ∴
∴ ![]() .
.
∵ ![]() ,函数
,函数![]() 是奇函数,∴
是奇函数,∴![]()
∵ ![]() 在
在![]() 上为增函数,即
上为增函数,即 ![]() 对一切
对一切![]() 恒成立,
恒成立,
即![]() 在
在![]() 恒成立,有
恒成立,有![]() ,∴
,∴![]()
得 ![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]()
(2)假设存在正数![]() 符合,∵
符合,∵ ![]() 过
过![]() ∴
∴ ![]()
![]() ,
,
设![]() ,
, ![]()
(i) 若![]() ,则函数
,则函数![]() 在
在![]() 上最小值为1
上最小值为1
∵ 对称轴 ![]() ,
,![]() (舍)
(舍)
(ii) 若![]() ,则
,则![]() 在
在![]() 上恒成立,且最大为1,最小值大于0
上恒成立,且最大为1,最小值大于0
①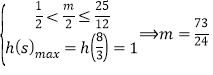
此时![]() ,
,![]() 故不合题意
故不合题意
②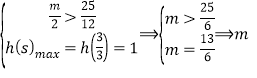 无解
无解
综上所述,不存在正数![]() 满足条件。
满足条件。


科目:高中数学 来源: 题型:
【题目】如图1,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 与
与![]() 的交点,以
的交点,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]() ,如图2.
,如图2.
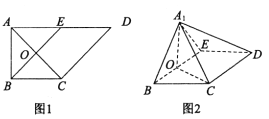
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】临川一中实验学校坐落在抚州火车站附近,在校区东边(如图),有一直径为8米的半圆形空地,现计划移植一古树,但需要有辅助光照.半圆周上的![]() 处恰有一可旋转光源满足古树生长的需要,该光源照射范围是
处恰有一可旋转光源满足古树生长的需要,该光源照射范围是![]() ,点
,点![]() 在直径
在直径![]() 上,且
上,且![]() .
.
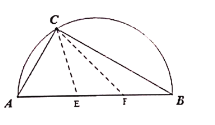
(1)若![]() ,求
,求![]() 的长;
的长;
(2)设![]() ,求该空地种植古树的最大面积.
,求该空地种植古树的最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了变废为宝,节约资源,新上了一个从生活垃圾中提炼生物柴油的项目.经测算该项目月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可以近似地表示为:
(吨)之间的函数关系可以近似地表示为: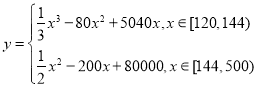 ,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为
,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为![]() 元,若该项目不获利,政府将给予补贴.
元,若该项目不获利,政府将给予补贴.
(1)当![]() 时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?
时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正四棱柱![]() 中,底面边长为
中,底面边长为![]() ,侧棱长为
,侧棱长为![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成的角的正弦值;
所成的角的正弦值;
(3)设![]() 为截面
为截面![]() 内-点(不包括边界),求
内-点(不包括边界),求![]() 到面
到面![]() ,面
,面![]() ,面
,面![]() 的距离平方和的最小值.
的距离平方和的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求k的值;
(2)设g(x)=log4![]() ,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角三棱柱![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() .
.
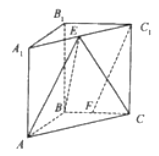
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)若直线![]() 和平面
和平面![]() 所成角的正弦值等于
所成角的正弦值等于![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】砂糖橘是柑橘类的名优品种,因其味甜如砂糖故名.某果农选取一片山地种植砂糖橘,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的![]() 倍.
倍.

(1)求a,b的值;
(2)从样本中产量在区间(50,60]上的果树里随机抽取两株,求产量在区间(55,60]上的果树至少有一株被抽中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com