(2011•潍坊二模)2011年3月,日本发生了9.0级地震,地震引发了海啸及核泄漏.某国际组织用分层抽样的方法从心理专家、核专家、地质专家三类专家中抽取若干人组成研究小组赴日本工作,有关数据见表1(单位:人).
核专家为了检测当地动物受核辐射后对身体健康的影响,随机选取了110只羊进行了检测,并将有关数据整理为不完整的2×2列联表(表2).
|
相关人员数 |
抽取人数 |
| 心理专家 |
24 |
x |
| 核专家 |
48 |
y |
| 地质专家 |
72 |
6 |
|
高度辐射 |
轻微辐射 |
合计 |
| 身体健康 |
30 |
A |
50 |
| 身体不健康 |
B |
10 |
60 |
| 合计 |
C |
D |
E |
附:临界值表
| k0 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
| P(K2≥k0) |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
参考公式:
K2=| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
;
(1)求研究小组的总人数;
(2)写出表2中A、B、C、D、E的值,并判断有多大的把握认为羊受到高度辐射与身体不健康有关;
(3)若从研究小组的心理专家和核专家中随机选2人撰写研究报告,求其中恰好有1人为心理专家的概率.



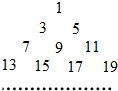 (2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是
(2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是 (2011•潍坊二模)运行如图的程序框图,当输入m=-4时的输出结果为n,若变量x,y满足
(2011•潍坊二模)运行如图的程序框图,当输入m=-4时的输出结果为n,若变量x,y满足