
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
| 顾客数(人) | x | 30 | 25 | y | 10 |
| 结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
| X | 1 | 1.5 | 2 | 2.5 | 3 |
| P |  |  |  | 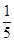 | 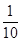 |

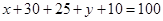 ,由100位顾客中一次购物量超过8件的顾客占55%,则知
,由100位顾客中一次购物量超过8件的顾客占55%,则知 .根据这两式得x=15,y=20,由表格可得X的可以取值为:1,1.5,2,2.5,3;该超市所有顾客一次购物的结算时间组成一个总体,所收集的100位顾客一次购物的结算时间可视为总体的一个容量为100的简单随机样本,将频率视为概率,即可得到分布列与期望.
.根据这两式得x=15,y=20,由表格可得X的可以取值为:1,1.5,2,2.5,3;该超市所有顾客一次购物的结算时间组成一个总体,所收集的100位顾客一次购物的结算时间可视为总体的一个容量为100的简单随机样本,将频率视为概率,即可得到分布列与期望. ×
× +
+ ×
× +
+ ×
× =
= .
. =
= ,P(X=1.5)=
,P(X=1.5)= =
= ,P(X=2)=
,P(X=2)= =
= ,
,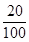 =
=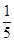 ,P(X=3)=
,P(X=3)=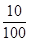 =
=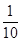 .
.| X | 1 | 1.5 | 2 | 2.5 | 3 |
| P |  |  |  | 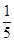 | 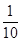 |
 +1.5×
+1.5× +2×
+2× +2.5×
+2.5×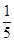 +3×
+3×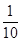 =1.9.
=1.9. ×
× +
+ ×
× +
+ ×
× =
= .
. .
.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
 店经销
店经销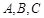 三种排量的汽车,其中
三种排量的汽车,其中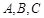 三种排量的汽车依次有5,4,3款不同车型.某单位计划购买3辆不同车型的汽车,且购买每款车型等可能.
三种排量的汽车依次有5,4,3款不同车型.某单位计划购买3辆不同车型的汽车,且购买每款车型等可能.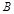 种排量汽车的概率;
种排量汽车的概率;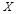 ,求
,求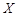 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
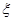 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
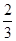 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,参加第五项不合格的概率为
,参加第五项不合格的概率为 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 版本 | 人教A版 | 人教B版 | ||
| 性别 | 男教师 | 女教师 | 男教师 | 女教师 |
| 人数 | 6 | 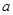 | 4 | 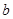 |
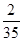 .且
.且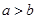 .
.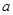 ,
,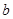 的值
的值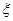 ,求随机变量
,求随机变量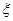 的分布列和数学期望
的分布列和数学期望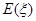 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com