
【题目】已知椭圆![]() 的中心在坐标原点,焦点在坐标轴上,焦距长为2,左准线为
的中心在坐标原点,焦点在坐标轴上,焦距长为2,左准线为![]() :
: ![]() .
.
(1)求椭圆![]() 的方程及其离心率;
的方程及其离心率;
(2)若过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,且
两点,且![]() 为线段
为线段![]() 的中点,求直线
的中点,求直线![]() 的方程;
的方程;
(3)过椭圆![]() 右准线
右准线![]() 上任一点
上任一点![]() 引圆
引圆![]() :
: ![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
, ![]() .试探究直线
.试探究直线![]() 是否过定点?若过定点,请求出该定点;否则,请说明理由.
是否过定点?若过定点,请求出该定点;否则,请说明理由.
【答案】(1)![]() ,
, ![]() (2)
(2)![]() (3)
(3)![]() .
.
【解析】试题分析:(1)根据条件可得关于a,b,c方程组,解得![]() ,
, ![]() ,即得椭圆
,即得椭圆![]() 的方程及其离心率;(2)利用点差法得中点坐标与弦斜率关系式,解得斜率,根据点斜式得直线
的方程及其离心率;(2)利用点差法得中点坐标与弦斜率关系式,解得斜率,根据点斜式得直线![]() 的方程;(3)先根据两圆:以
的方程;(3)先根据两圆:以![]() 为直径的圆与圆
为直径的圆与圆![]() 方程相减得切点弦
方程相减得切点弦![]() 方程,再根据方程恒等得定点
方程,再根据方程恒等得定点
试题解析:(1)设椭圆![]() 方程为
方程为![]() ,则
,则![]() ,所以
,所以![]() ,
,
又其准线为![]() ,所以
,所以![]() ,则
,则![]() ,
,
所以椭圆![]() 方程为
方程为![]() ,其离心率为
,其离心率为![]() .
.
(2)设点![]() 和点
和点![]() 坐标分别为
坐标分别为![]() ,
, ![]() ,因为点
,因为点![]() 和点
和点![]() 都在椭圆上,
都在椭圆上,
所以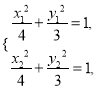 两式相减得
两式相减得![]() ,
,
又点![]() 为线段
为线段![]() 的中点,所以
的中点,所以![]() ,
, ![]() ,
,
所以直线![]() 的斜率为
的斜率为![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
(3)直线![]() 恒过定点
恒过定点![]() .
.
因为椭圆的右准线方程为![]() ,所以设
,所以设![]() 点坐标为
点坐标为![]() ,圆心
,圆心![]() 坐标为
坐标为![]() ,
,
因为直线![]() ,
, ![]() 是圆
是圆![]() 的两条切线,所以切点
的两条切线,所以切点![]() ,
, ![]() 在以
在以![]() 为直径的圆上.
为直径的圆上.
所以该圆方程为![]() ,
,
两圆方程相减,得直线![]() 的方程
的方程![]() ,
,
即![]() ,由
,由![]() 得
得![]()
所以直线![]() 必过定点
必过定点![]() .
.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(﹣x)=f(x),f(x+8)=f(x),且当x∈(0,4]时f(x)= ![]() ,关于x的不等式f2(x)+af(x)>0在[﹣2016,2016]上有且只有2016个整数解,则实数a的取值范围是( )
,关于x的不等式f2(x)+af(x)>0在[﹣2016,2016]上有且只有2016个整数解,则实数a的取值范围是( )
A.(﹣ ![]() ln6,ln2]
ln6,ln2]
B.(﹣ln2,﹣ ![]() ln6)
ln6)
C.(﹣ln2,﹣ ![]() ln6]
ln6]
D.(﹣ ![]() ln6,ln2)
ln6,ln2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,平行四边形ABCD中,AB=2AD,∠DAB=60°,M是BC的中点.将△ADM沿DM折起,使面ADM⊥面MBCD,N是CD的中点,图2所示. 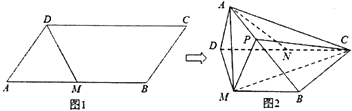
(Ⅰ)求证:CM⊥平面ADM;
(Ⅱ)若P是棱AB上的动点,当 ![]() 为何值时,二面角P﹣MC﹣B的大小为60°.
为何值时,二面角P﹣MC﹣B的大小为60°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
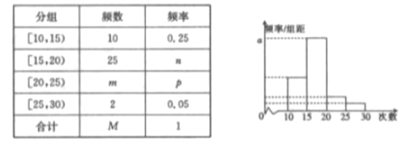
(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)若该校高一学生有800人,试估计该校高一学生参加社区服务的次数在区间![]() 内的人数.
内的人数.
【答案】(1)![]() ,
, ![]() ,
, ![]() ;(2)
;(2)![]() 人.
人.
【解析】试题分析:(1)由题意, ![]() 内的频数是10,频率是0.25知,
内的频数是10,频率是0.25知, ![]() ,所以
,所以![]() ,则
,则![]() ,
, ![]() .(2)高一学生有800人,分组
.(2)高一学生有800人,分组![]() 内的频率是
内的频率是![]() ,人数为
,人数为![]() 人.
人.
试题解析:
(1)由![]() 内的频数是10,频率是0.25知,
内的频数是10,频率是0.25知, ![]() ,所以
,所以![]() .
.
因为频数之和为40,所以![]() ,
, ![]() .
.
![]() .
.
因为![]() 是对应分组
是对应分组![]() 的频率与组距的商,所以
的频率与组距的商,所以![]() .
.
(2)因为该校高一学生有800人,分组![]() 内的频率是
内的频率是![]() ,
,
所以估计该校高一学生参加社区服务的次数在此区间内的人数为![]() 人.
人.
【题型】解答题
【结束】
18
【题目】已知直线![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() ,且与
,且与![]() 交于
交于![]() 两点.
两点.
(1)设![]() 为
为![]() 上一动点,
上一动点, ![]() 到直线
到直线![]() 的距离为
的距离为![]() ,点
,点![]() ,求
,求![]() 的最小值;
的最小值;
(2)求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司引进一条价值30万元的产品生产线,经过预测和计算,得到生产成本降低![]() 万元与技术改造投入
万元与技术改造投入![]() 万元之间满足:①
万元之间满足:①![]() 与
与![]() 和
和![]() 的乘积成正比;②当
的乘积成正比;②当![]() 时,
时, ![]() ,并且技术改造投入比率
,并且技术改造投入比率![]() ,
, ![]() 为常数且
为常数且![]() .
.
(1)求![]() 的解析式及其定义域;
的解析式及其定义域;
(2)求![]() 的最大值及相应的
的最大值及相应的![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,
, ![]() (其中
(其中![]() 是自然对数的底数).
是自然对数的底数).
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求实数
垂直,求实数![]() 的值;
的值;
(2)记函数![]() ,其中
,其中![]() ,若函数
,若函数![]() 在
在![]() 内存在两个极值点,求实数
内存在两个极值点,求实数![]() 的取值范围;
的取值范围;
(3)若对任意![]() ,
, ![]() ,且
,且![]() ,均有
,均有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于实数x,符号[x]表示不超过x的最大整数,例如[π]=3,[﹣1.08]=﹣2,定义函数f(x)=x﹣[x],则下列命题中正确的是
①函数f(x)的最大值为1; ②函数f(x)的最小值为0;
③方程![]() 有无数个根; ④函数f(x)是增函数.
有无数个根; ④函数f(x)是增函数.
A. ②③ B. ①②③ C. ② D. ③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为(-3,3),
满足f(-x)=-f(x),且对任意x,y,都有f(x)-f(y)=f(x-y),当x<0时,f(x)>0,f(1)=-2.
(1)求f(2)的值;
(2)判断f(x)的单调性,并证明;
(3)若函数g(x)=f(x-1)+f(3-2x),求不等式g(x)≤0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE= ![]() BB1 , C1F=
BB1 , C1F= ![]() CC1 .
CC1 . 
(1)求平面AEF与平面ABC所成角α的余弦值;
(2)若G为BC的中点,A1G与平面AEF交于H,且设 ![]() =
= ![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com