
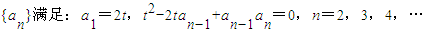 (其中t为常数且t≠0).
(其中t为常数且t≠0).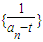 为等差数列;
为等差数列;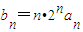 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.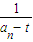 -
-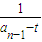 =
= (为常数),由此得出结论.
(为常数),由此得出结论. =
=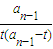 ,即
,即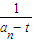 =
=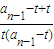 =
= +
+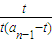 ,
,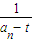 -
-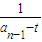 =
= (为常数),∴数列
(为常数),∴数列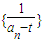 为等差数列.
为等差数列. 为等差数列.公差为
为等差数列.公差为 ,∴
,∴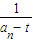 =
=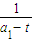 +(n-1)
+(n-1) =
=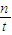 .
. +t.
+t.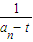 -
-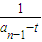 =
= (为常数),(2)的关键是熟练掌握等差数列的通项公式,(3)的关键是根据数列{bn}的通项公式确定使用错位相减法进行数列求和,属于中档题.
(为常数),(2)的关键是熟练掌握等差数列的通项公式,(3)的关键是根据数列{bn}的通项公式确定使用错位相减法进行数列求和,属于中档题. 

 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
| t |
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 ;②f(x)是奇函数;③f(x)是周期函数且一个周期为4t;④f(x)在(0,2t)内为单调函数.其中正确命题的序号是________.
;②f(x)是奇函数;③f(x)是周期函数且一个周期为4t;④f(x)在(0,2t)内为单调函数.其中正确命题的序号是________.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| t |
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省乐山一中高三(上)9月月考数学试卷(文科)(解析版) 题型:填空题
 ;②f(x)是奇函数;③f(x)是周期函数且一个周期为4t;④f(x)在(0,2t)内为单调函数.其中正确命题的序号是 .
;②f(x)是奇函数;③f(x)是周期函数且一个周期为4t;④f(x)在(0,2t)内为单调函数.其中正确命题的序号是 .查看答案和解析>>
科目:高中数学 来源:2012年四川省高考数学压轴卷(理科)(解析版) 题型:解答题
 ;②f(x)是奇函数;③f(x)是周期函数且一个周期为4t;④f(x)在(0,2t)内为单调函数.其中正确命题的序号是 .
;②f(x)是奇函数;③f(x)是周期函数且一个周期为4t;④f(x)在(0,2t)内为单调函数.其中正确命题的序号是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com