
| x-1 |
| 2 |
| a3 |
| b4+b6 |
| a7 |
| b2+b8 |
| 2 |
| 5 |
| Sn |
| Tn |
| An+1 |
| 2n+7 |
|
| a5 |
| b5 |
| 2 |
| 5 |
| Sn |
| Tn |
| An+1 |
| 2n+7 |
| Sn |
| Tn |
| An+1 |
| 2n+7 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a3 |
| b4+b6 |
| a7 |
| b2+b8 |
| 2 |
| 5 |
| a5 |
| b5 |
| 2 |
| 5 |
| S9 |
| T9 |
| ||
|
| a5 |
| b5 |
| 2 |
| 5 |
| Sn |
| Tn |
| An+1 |
| 2n+7 |
| 9A+1 |
| 2×9+7 |
| 2 |
| 5 |
| Sn |
| Tn |
| n+1 |
| 2n+7 |
| n(n+1) |
| n(2n+7) |
| 4 |
| 3 |
| 1 |
| 4 |
| n2+n+2 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 4 |
| n2-n |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| mx |
| x2+n |
| a |
| x |
| 7 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| f2(x2)-f2(x1) |
| x2-x1 |
| b |
| 3 |
| y2-y1 |
| x2-x1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
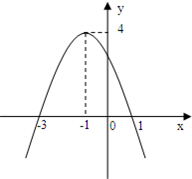 如图是一个二次函数y=f(x)的图象
如图是一个二次函数y=f(x)的图象| f(x)+2x | x |
查看答案和解析>>
科目:高中数学 来源:大连市第八中学2006~2007学年度下学期高二理科数学试卷 题型:044
定义一组函数fn(x)=(1+x)n-1(x>-2),n∈N,且n≥2,其导函数记为![]()
(1)求证:fn(x)≥nx
(2)设![]() ,求证:0<x0<1
,求证:0<x0<1
(3)设函数g(x)=f3(x)-f2(x),[a,b]![]() ,g(x)在区间[a,b]上的值域为[ka,kb],求出k的最小值及相应的区间[a,b].
,g(x)在区间[a,b]上的值域为[ka,kb],求出k的最小值及相应的区间[a,b].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com