
【题目】如图,为迎接校庆,我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1 , 种花的面积为S2 , 比值 ![]() 称为“规划和谐度”.
称为“规划和谐度”.
(1)试用a,θ表示S1 , S2;
(2)若a为定值,BC足够长,当θ为何值时,“规划和谐度”有最小值,最小值是多少?
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在斜三棱柱ABC﹣A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在面ABC上的射影H必在( ) 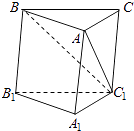
A.直线AB上
B.直线BC上
C.直线CA上
D.△ABC内部
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈[1,2],x2﹣a≥0;命题q:x0∈R,使得 ![]() +(a﹣1)x0+1<0.若“p或q”为真,“p且q”为假,则实数a的取值范围
+(a﹣1)x0+1<0.若“p或q”为真,“p且q”为假,则实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c. (Ⅰ)求C;
(Ⅱ)若c= ![]() ,△ABC的面积为
,△ABC的面积为 ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,再将整个图象沿x轴向右平移 ![]() 个单位,沿y轴向下平移1个单位,得到函数y=
个单位,沿y轴向下平移1个单位,得到函数y= ![]() sinx的图象,则y=f(x)的解析式为( )
sinx的图象,则y=f(x)的解析式为( )
A.y= ![]() sin(2x+
sin(2x+ ![]() )+1
)+1
B.y= ![]() sin(2x﹣
sin(2x﹣ ![]() )+1
)+1
C.y= ![]() sin(
sin( ![]() x+
x+ ![]() )+1
)+1
D.y= ![]() sin(
sin( ![]() x﹣
x﹣ ![]() )+1
)+1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次马拉松比赛中,30名运动员的成绩(单位:分钟)的茎叶图如图所示.若将运动员按成绩由好到差编号为1﹣30号,再用系统抽样方法从中抽取6人,则其中成绩在区间[130,151]上的运动员人数是( ) 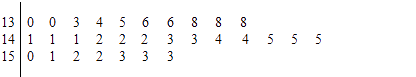
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:m∈{x|x2+(a﹣8)x﹣8a≤0},命题q:方程 ![]() =1表示焦点在x轴上的双曲线.
=1表示焦点在x轴上的双曲线.
(1)若当a=1时,命题p∧q假命题,p∨q”为真命题,求实数m的取值范围;
(2)若命题p是命题q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x2+x+m)ex(其中m∈R,e为自然对数的底数).若在x=﹣3处函数f (x)有极大值,则函数f (x)的极小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次考试中,五位学生的数学,物理成绩如下表所示:

(1)要从5名学生中选2人参加一项活动,求选中的学生中至少有一人的物理成绩高于90分的概率;

(2)根据上表数据,画出散点图并用散点图说明物理成绩![]() 与数学成绩
与数学成绩![]() 之间线性相关关系的强弱,如果具有较强的线性相关关系,求
之间线性相关关系的强弱,如果具有较强的线性相关关系,求![]() 与
与![]() 的线性回归方程(系数精确到0.01);如果不具有线性相关关系,请说明理由.
的线性回归方程(系数精确到0.01);如果不具有线性相关关系,请说明理由.
参考公式:
回归直线的方程是![]() ,其中
,其中 ,
, ![]() ,
,
![]() 是与
是与![]() 对应的回归估计值,
对应的回归估计值,
参考数据: ![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com