已知函数f(x)=(x2+ax+b)ex,x=1是它的一个极值点.
(I)求函数f(x)的单调区间;
(II)当x≥3时,关于x的不等式f(x)≤e2x恒成立,求实数a的取值范围.
解:(I)f′(x)=(2x+a)e
x+(x
2+ax+b)e
x=e
x[x
2+(2+a)x+a+b]
由题意知f′(1)=0,即3+2a+b=0,b=-2a-3.
f(x)=e
x[x
2+(2+a)x-a-3]=e
x(x-1)(x+a+3),
∵x=1是函数的一个极值点,∴-a-3≠1,a≠-4
当a<-4时,由f′(x)<0得1<x<-a-3
∴f(x)的单调增区间为(-∞,1),(-a-3,+∞),减区间为(1,-a-3),
当a>-4时,由f′(x)<0得-a-3<x<1
∴f(x)的单调增区间为(-∞,-a-3),(1,+∞),减区间为(-a-3,1).
(II)f(x)≤e
2x,得 x
2+ax-2a-3≤e
x,(x-2)a≤e
x-x
2+3,
得:
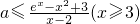
令g(x)=
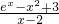
,则

令h(x)=e
x-x+1,则h′(x)=e
x-1.
当x≥3时,e
x-1>0,即:h(x)≥h(3)=e
3-2>0,
∴g′(x)>0,即x≥3时,g(x)为增函数,
∴

∴a≤e
3-6,又a≠-4,
∴实数a的取值范围是:(-∞,-4)∪(-4,e
3-6].
分析:(I)首要的是求出函数的导数,利用已知函数在x=1处取得极值,可以建立参数a,b的关系,从而利用a表达出b,另外x=1是极值点可得a≠-4,因此要注意对a进行讨论:a<-4和a>-4.
(II)对于这类含参数的不等式恒成立问题,可以转化为函数的最值问题来求解,由f(x)≤e
2x,得:
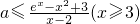
,因此构造函数是很容易想到的,即:令g(x)=
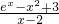
,然后求解即可.
点评:本题考查了函数的导数及其应用,利用导数求函数的单调区间,对函数的极值的研究,求解一类含参不等式的恒成立问题,是一道很好的综合问题,本题涉及的思想方法有分类讨论思想,转会与化归思想,构造法等.

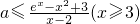
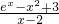 ,则
,则

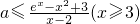 ,因此构造函数是很容易想到的,即:令g(x)=
,因此构造函数是很容易想到的,即:令g(x)=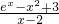 ,然后求解即可.
,然后求解即可.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案