
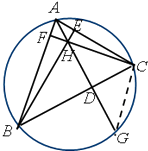
【题目】如图,已知AD、BE、CF分别是△ABC三边的高,H是垂心,AD的延长线交△ABC的外接圆于点G. 
(1)求证:∠CHG=∠ABC;
(2)求证:ABGD=ADHC.
【答案】
(1)证明:∵AD、CF分别是△ABC三边的高,
∴AD⊥BC,CF⊥AB,
即有∠HDB=∠HFB=90°,
可得四点H,F,B,D共圆,
由圆内接四边形的性质可得,
∠CHG=∠ABC.
(2)证明:连结CG,
∵∠ABC与∠AGC同弧圆周角,
∴∠ABC=∠AGC,
∵∠CHG=∠ABC,
∴∠CHG=∠AGC,
∴GC=HC,
在Rt△ADB和Rt△GDC中,
∵∠ABC=∠AGC,即∠ABD=∠CGD,
∴Rt△ADB∽Rt△GDC,
∴ ![]() ,
,
∴ABGD=ADGC,
又∵GC=HC,
∴ABGD=ADHC.
【解析】(1)由三角形的高的定义,可得∠HDB=∠HFB=90°,则四点H,F,B,D共圆,由圆内接四边形的性质,即可得证;(2)连结CG,由同弧所对圆周角相等,证得Rt△ADB∽Rt△GDC,由相似三角形的性质:对应边成比例,即可得证.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某学生对其30位亲属的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主).

(1)根据茎叶图,帮助这位同学说明这30位亲属的饮食习惯.
(2)根据以上数据完成如下2×2列联表.

(3)能否有99%的把握认为其亲属的饮食习惯与年龄有关?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆x2+y2=1上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(1)写出C的参数方程;
(2)设直线l:2x+y﹣2=0与C的交点为P1 , P2 , 以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1P2的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,平面
为正方形,平面![]() 底面
底面![]() ,
, ![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() 平面
平面![]() ;
;
(Ⅲ)在棱![]() 上求作一点
上求作一点![]() ,使得
,使得![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,从参加环保知识竞赛的学生中抽出40名,将其成绩(均为整数)整理后画出的频率分布直方图如下:

观察图形,回答下列问题:
(1)估计这次环保知识竞赛成绩的中位数;
(2)从成绩是80分以上(包括80分)的学生中选两人,求他们在同一分数段的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若a,b,c∈R,f(a),f(b),f(c)为某一三角形的三边长,则称f(x)为“可构造三角形函数”.已知函数f(x)=![]() 是“可构造三角形函数”,则实数t的取值范围是( )
是“可构造三角形函数”,则实数t的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从2016年1月1日起,广东、湖北等18个保监局所辖地区将纳入商业车险改革试点范围,其中最大的变化是上一年的出险次数决定了下一年的保费倍率,具体关系如表:
上一年的 | 0 | 1 | 2 | 3 | 4 | 5次以上(含5次) |
下一年 | 85% | 100% | 125% | 150% | 175% | 200% |
连续两年没有出险打7折,连续三年没有出险打6折 | ||||||
有评估机构从以往购买了车险的车辆中随机抽取1000辆调查,得到一年中出险次数的频数分布如下(并用相应频率估计车辆每年出险次数的概率):
一年中出险次数 | 0 | 1 | 2 | 3 | 4 | 5次以上(含5次) |
频数 | 500 | 380 | 100 | 15 | 4 | 1 |
(1)求某车在两年中出险次数不超过2次的概率;
(2)经验表明新车商业车险保费与购车价格有较强的线性相关关系,估计其回归直线方程为: ![]() =120x+1600.(其中x(万元)表示购车价格,y(元)表示商业车险保费).李先生2016 年1月购买一辆价值20万元的新车.根据以上信息,试估计该车辆在2017 年1月续保时应缴交的保费,并分析车险新政是否总体上减轻了车主负担.(假设车辆下一年与上一年都购买相同的商业车险产品进行续保)
=120x+1600.(其中x(万元)表示购车价格,y(元)表示商业车险保费).李先生2016 年1月购买一辆价值20万元的新车.根据以上信息,试估计该车辆在2017 年1月续保时应缴交的保费,并分析车险新政是否总体上减轻了车主负担.(假设车辆下一年与上一年都购买相同的商业车险产品进行续保)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com