

【题目】已知函数![]() .
.
(1)求函数![]() 的的单调区间;
的的单调区间;
(2)若![]() 恒成立,试确定实数
恒成立,试确定实数![]() 的取值范围;
的取值范围;
(3)证明:![]() .
.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上是增函数,当
上是增函数,当![]() 时,
时,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数;(2)
上是减函数;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:(1)函数![]() 的定义域为
的定义域为![]() ,分
,分![]() 和
和![]() 两种情况分类讨论,即可求解函数的单调性;(2)由(1)知
两种情况分类讨论,即可求解函数的单调性;(2)由(1)知![]() 时,
时,![]() 不成立,故
不成立,故![]() ,又由(1)知
,又由(1)知![]() 的最大值为
的最大值为![]() ,只需
,只需![]() 即可,即可求解
即可,即可求解![]() ;(3)由(2)知,当
;(3)由(2)知,当![]() 时,有
时,有![]() 在
在![]() 恒成立,且
恒成立,且![]() 在
在![]() 上是减函数,进而
上是减函数,进而![]() ,则
,则![]() ,即
,即![]() ,即可证明结论.
,即可证明结论.
试题解析:(1) 函数![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上是增函数,
上是增函数,
当![]() 时,若
时,若![]() 时,有
时,有![]() ,
,
若![]() 时,有
时,有![]() ,则
,则![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
(2)由(1)知![]() 时,
时,![]() 在
在![]() 上是增函数,而
上是增函数,而![]() 不成立,故
不成立,故![]() ,又由(1)知
,又由(1)知![]() 的最大值为
的最大值为![]() ,要使
,要使![]() 恒成立,则
恒成立,则![]() 即可,
即可,
即![]() ,得
,得![]() .
.
(3)由(2)知,当![]() 时,有
时,有![]() 在
在![]() 恒成立,且
恒成立,且![]() 在
在![]() 上是减函数,
上是减函数,
![]() ,即
,即![]() ,在
,在![]() 上恒成立,令
上恒成立,令![]() ,则
,则![]() ,
,
即![]() ,从而
,从而
![]() 得证.
得证.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数);在以原点
为参数);在以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(II)若射线![]() 与曲线
与曲线![]() ,
,![]() 的交点分别为
的交点分别为![]() (
(![]() 异于原点),当斜率
异于原点),当斜率![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了迎接世博会,某旅游区提倡低碳生活,在景区提供自行车出租.该景区有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元.根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超出6元,则每超过1元,租不出的自行车就增加3辆.为了便于结算,每辆自行车的日租金![]() (元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用
(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用![]() (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得)。
(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得)。
(1)求函数![]() 的解析式及其定义域;
的解析式及其定义域;
(2)试问当每辆自行车的日租金定为多少元时,才能使一日的净收入最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与短轴的两个端点是正三角形的三个项点,点
的一个焦点与短轴的两个端点是正三角形的三个项点,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设不过原点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥P-ABC中,∠ACB=90°,CB=4,AB=20,D为AB中点,M为PB中点,且△PDB是正三角形,PA⊥PC。
 .
.
(1)求证:DM∥平面PAC;
(2)求证:平面PAC⊥平面ABC;
(3)求三棱锥M-BCD的体积
查看答案和解析>>
科目:高中数学 来源: 题型:
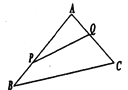
【题目】如图,某生态园将一三角形地块![]() 的一角
的一角![]() 开辟为水果园种植桃树,已知角
开辟为水果园种植桃树,已知角![]() 为
为![]() ,
,![]() 的长度均大于
的长度均大于![]() 米,现在边界
米,现在边界![]() 处建围墙,在
处建围墙,在![]() 处围竹篱笆.
处围竹篱笆.
(1)若围墙![]() 总 长度为
总 长度为![]() 米,如何围可使得三角形地块
米,如何围可使得三角形地块![]() 的面积最大?
的面积最大?
(2)已知![]() 段围墙高
段围墙高![]() 米,
米,![]() 段围墙高
段围墙高![]() 米,造价均为每平方米
米,造价均为每平方米![]() 元.若围围墙用了
元.若围围墙用了![]() 元,问如何围可使竹篱笆用料最省?
元,问如何围可使竹篱笆用料最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东![]() 且与点A相距40
且与点A相距40![]() 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东![]() +
+![]() (其中sin
(其中sin![]() =
=![]() ,
,![]() )且与点A相距10
)且与点A相距10![]() 海里的位置C.
海里的位置C.
(I)求该船的行驶速度(单位:海里/小时);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com