
【题目】甲、乙两同学在复习数列时发现原来曾经做过的一道数列问题因纸张被破坏,导致一个条件看不清,具体如下:等比数列![]() 的前n项和为
的前n项和为![]() ,已知_____,
,已知_____,
(1)判断![]() ,
,![]() ,
,![]() 的关系;
的关系;
(2)若![]() ,设
,设![]() ,记
,记![]() 的前n项和为
的前n项和为![]() ,证明:
,证明:![]() .
.
甲同学记得缺少的条件是首项a1的值,乙同学记得缺少的条件是公比q的值,并且他俩都记得第(1)问的答案是![]() ,
,![]() ,
,![]() 成等差数列.如果甲、乙两同学记得的答案是正确的,请你通过推理把条件补充完整并解答此题.
成等差数列.如果甲、乙两同学记得的答案是正确的,请你通过推理把条件补充完整并解答此题.
科目:高中数学 来源: 题型:
【题目】刍甍,中国古代算术中的一种几何图形,《九章算术》中记载“刍甍者,下有褒有广,而上有褒无广”刍,草也;甍,屋盖也.翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱,刍甍字面意思为茅草屋顶”如图,为一刍甍的三视图,其中正视图为等腰梯形,侧视图为等腰三角形,若用茅草搭建它(无底面,不考虑厚度),则需要覆盖的面积至少为( )



A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,点E在BD上,EA=EB=EC=ED,BD![]() CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值
CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值![]() 时,三棱锥A﹣BCD的外接球的表面积为_____.
时,三棱锥A﹣BCD的外接球的表面积为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为2的等边![]() 中,
中,![]() 分别为边
分别为边![]() 的中点,将AED沿
的中点,将AED沿![]() 折起,使得
折起,使得![]() ,
, ![]() ,得到如图2的四棱锥A-BCDE,连结
,得到如图2的四棱锥A-BCDE,连结![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() .
.
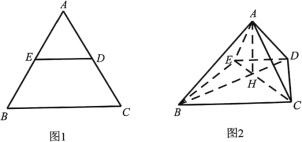
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列说法:①“![]() ”是“
”是“![]() ”的充分不必要条件;②命题“
”的充分不必要条件;②命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;③小赵、小钱、小孙、小李到4个景点旅游,每人只去一个景点,设事件
”;③小赵、小钱、小孙、小李到4个景点旅游,每人只去一个景点,设事件![]() 为“4个人去的景点不相同”,事件
为“4个人去的景点不相同”,事件![]() 为“小赵独自去一个景点”,则
为“小赵独自去一个景点”,则![]() ;④设
;④设![]() ,其正态分布密度曲线如图所示,那么向正方形
,其正态分布密度曲线如图所示,那么向正方形![]() 中随机投掷10000个点,则落入阴影部分的点的个数的估计值是6587.(注:若
中随机投掷10000个点,则落入阴影部分的点的个数的估计值是6587.(注:若![]() ,则
,则![]() ,
,![]() )其中正确说法的个数为( )
)其中正确说法的个数为( )
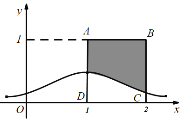
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自由购是通过自助结算方式购物的一种形式. 某大型超市为调查顾客使用自由购的情况,随机抽取了100人,统计结果整理如下:
20以下 |
|
|
|
|
| 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(Ⅰ)现随机抽取 1 名顾客,试估计该顾客年龄在![]() 且未使用自由购的概率;
且未使用自由购的概率;
(Ⅱ)从被抽取的年龄在![]() 使用自由购的顾客中,随机抽取3人进一步了解情况,用
使用自由购的顾客中,随机抽取3人进一步了解情况,用![]() 表示这3人中年龄在
表示这3人中年龄在![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)为鼓励顾客使用自由购,该超市拟对使用自由购的顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为椭圆
的焦点为椭圆![]() 的右焦点,C的准线与E交于P,Q两点,且
的右焦点,C的准线与E交于P,Q两点,且![]() .
.
(1)求E的方程;
(2)过E的左顶点A作直线l交E于另一点B,且BO(O为坐标原点)的延长线交E于点M,若直线AM的斜率为1,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校团委对“学生性别与中学生追星是否有关”作了一次调查,利用![]() 列联表,由计算得
列联表,由计算得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
得到正确结论是( )
A. 有99%以上的把握认为“学生性别与中学生追星无关”
B. 有99%以上的把握认为“学生性别与中学生追星有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“学生性别与中学生追星无关”
D. 在犯错误的概率不超过0.5%的前提下,认为“学生性别与中学生追星有关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com